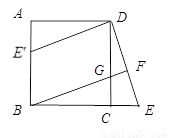
题目内容
如图,在正方形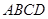 中,
中,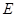 是
是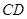 边上的中点,
边上的中点,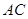 与
与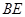 相交于点
相交于点 ,连接
,连接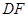 .(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角).
.(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角).
(1) 在不增加点和线的前提下,直接写出图中所有的全等三角形.(不要求证明)
(2) 连接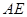 试判断
试判断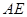 与
与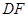 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(3)延长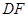 交
交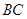 于点
于点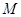 ,试判断
,试判断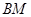 与
与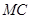 的数量关系,并说明理由.
的数量关系,并说明理由.
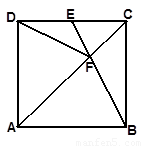
(1)△ABC≌△ADC,△ABF≌△ADF,△BCF≌△DCF;(2)AE⊥DF;(3)BM=MC.
【解析】
试题分析:(1)根据正方形的性质得到相关的条件即可找出全等的三角形;
(2)可证△BCF≌△DCF得∠CBF=∠CDF,再证△ADE≌△BCE得∠DAE=∠CBE,故∠DAE=∠CDF,又∠DAE+∠AED=90°,则∠CDF +∠AED=90°,即AE⊥DF;
(3)可证△DCM≌△BCE得CE=CM,又CE=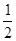 CD,CD=BC,故CM=
CD,CD=BC,故CM=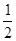 BC,即BM=MC.
BC,即BM=MC.
(1)△ADF≌△ABF,△ADC≌△ABC,△CDF≌△CBF;
(2)AE⊥DF.
证明:设AE与DF相交于点H.
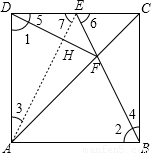
∵四边形ABCD是正方形,
∴AD=AB,∠DAF=∠BAF.
又∵AF=AF,
∴△ADF≌△ABF.
∴∠1=∠2.
又∵AD=BC,∠ADE=∠BCE=90°,DE=CE,
∴△ADE≌△BCE.
∴∠3=∠4.
∵∠2+∠4=90°,
∴∠1+∠3=90°,
∴∠AHD=90°.
∴AE⊥DF;
(3)如图所示:
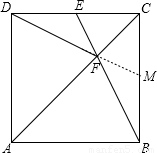
∵∠ADE=90°,AE⊥DF.
∴∠1+∠5=90°,∠3+∠1=90°.
∴∠3=∠5,
∵∠3=∠4,
∴∠4=∠5.
∵DC=BC,∠DCM=∠BCE=90°,
∴△DCM≌△BCE.
∴CE=CM,
又∵E为CD中点,且CD=CB,
∴CE=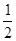 CD=
CD=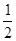 BC,
BC,
∴CM=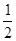 CB,即M为BC中点,
CB,即M为BC中点,
∴BM=MC.
考点:本题主要考查了正方形的性质和全等三角形的判定
点评:解答本题的关键是充分利用正方形的特殊性质来找到全等的条件,在判定全等后利用全等三角形的性质解题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案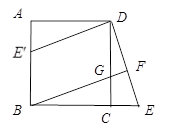
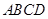 中,
中,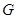 是
是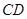 上一点,延长
上一点,延长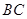 到
到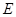 ,使
,使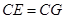 ,连接
,连接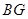 并延长交
并延长交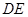 于
于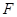 .
. ;(4分)
;(4分)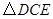 绕点
绕点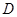 顺时针旋转
顺时针旋转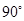 得到
得到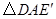 ,
,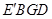 是什么特殊四边形?并说明理由.(6分)
是什么特殊四边形?并说明理由.(6分)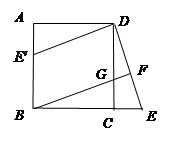
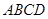 中,
中,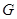 是
是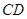 上一点,延长
上一点,延长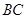 到
到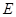 ,使
,使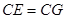 ,连接
,连接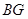 并延长交
并延长交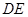 于
于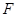 .
.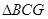 ≌
≌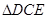 ;
;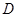 顺时针旋转
顺时针旋转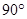 得到
得到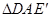 ,判断四边形
,判断四边形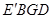 是什么特殊四边形?并说明理由.
是什么特殊四边形?并说明理由.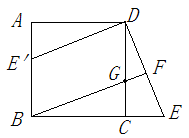
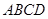 中,
中,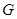 是
是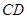 上一点,延长
上一点,延长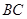 到
到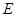 ,使
,使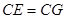 ,连接
,连接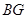 并延长交
并延长交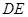 于
于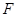 .
.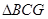 ≌
≌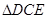 ;
;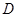 顺时针旋转
顺时针旋转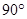 得到
得到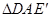 ,判断四边形
,判断四边形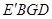 是什么特殊四边形?并说明理由.
是什么特殊四边形?并说明理由.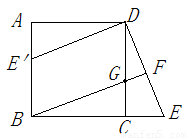
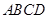 中,
中,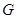 是
是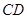 上一点,延长
上一点,延长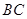 到
到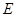 ,使
,使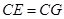 ,连接
,连接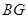 并延长交
并延长交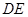 于
于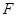 .
.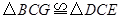 ;(4分)
;(4分)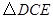 绕点
绕点 顺时针旋转
顺时针旋转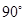 得到
得到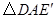 ,
,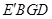 是什么特殊四边形?并说明理由.(6分)
是什么特殊四边形?并说明理由.(6分)