题目内容
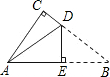
 一张直角三角形的纸片,像如图所示那样折叠,使两个锐角顶点A、B重合.若∠B=30°,
一张直角三角形的纸片,像如图所示那样折叠,使两个锐角顶点A、B重合.若∠B=30°,
AC= ,则折痕DE的长等于________.
,则折痕DE的长等于________.
1
分析:利用特殊角度构成特殊三角形,运用三角函数求解.
解答:由折叠的性质可得,点E是等腰三角形DAB的底边上的中点.
根据等腰三角形的性质知,DE⊥AB.
∵∠B=30°,AC= ,
,
∴AB=2 ,BE=
,BE= .
.
∴DE=BEtan30°=1.
点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
②等腰三角形的判定和性质,锐角三角函数的概念求解.
分析:利用特殊角度构成特殊三角形,运用三角函数求解.
解答:由折叠的性质可得,点E是等腰三角形DAB的底边上的中点.
根据等腰三角形的性质知,DE⊥AB.
∵∠B=30°,AC=
 ,
,∴AB=2
 ,BE=
,BE= .
.∴DE=BEtan30°=1.
点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
②等腰三角形的判定和性质,锐角三角函数的概念求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )| A、4cm | B、5cm | C、6cm | D、10cm |
 如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.
如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长. 一张直角三角形的纸片,像如图所示那样折叠,使两个锐角顶点A、B重合.若∠B=30°,
一张直角三角形的纸片,像如图所示那样折叠,使两个锐角顶点A、B重合.若∠B=30°, (2012•香坊区一模)如图是一张直角三角形的纸片.两直角边AC=6cm,BC=8cm将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )
(2012•香坊区一模)如图是一张直角三角形的纸片.两直角边AC=6cm,BC=8cm将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )