题目内容
7.在△ABC中,∠C=90°,AC=3,AB=4,则下列结论中,正确的是( )| A. | sinA=$\frac{3}{4}$ | B. | cosA=$\frac{3}{4}$ | C. | tanA=$\frac{3}{4}$ | D. | cotA=$\frac{3}{4}$ |
分析 首先利用勾股定理计算出BC的长,然后再根据三角函数定义进行分析即可.
解答 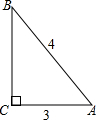 解:∵∠C=90°,AC=3,AB=4,
解:∵∠C=90°,AC=3,AB=4,
∴BC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{16-9}$=$\sqrt{7}$,
∴sinA=$\frac{BC}{AB}$=$\frac{\sqrt{7}}{4}$,故A错误,
cosA=$\frac{AC}{AB}$=$\frac{3}{4}$故B正确;
tanA=$\frac{CB}{AC}$=$\frac{\sqrt{7}}{3}$,故C错误;
cotA=$\frac{AC}{BC}$=$\frac{3}{\sqrt{7}}$=$\frac{3\sqrt{7}}{7}$,故D错误;
故选:B.
点评 此题主要多边形锐角三角函数,关键是掌握正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.正切:锐角A的对边a与邻边b的比叫做∠A的正切,余切:锐角A的邻边b与对边a的比叫做∠A的余切.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
15.下列式子正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\root{3}{9}$=3 | C. | $\sqrt{-4}$=-2 | D. | ±$\sqrt{16}$=±4 |
12.下列各组数中是勾股数的一组是( )
| A. | 1,2,$\sqrt{5}$ | B. | 1,2,$\sqrt{3}$ | C. | 9,12,15 | D. | 6,8,12 |
17.如果多项式x3-6x2-7与多项式3x3+mx2-5x+3的和不含二次项,则m等于( )
| A. | 6 | B. | -6 | C. | 3 | D. | -3 |
 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-3的解集是1<x<$\frac{5}{2}$.
如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-3的解集是1<x<$\frac{5}{2}$.