题目内容
在梯形ABCD中,AD∥BC,若∠BCD的平分线CH⊥AB于点H,BH=3AH,且四边形AHCD的面积为21,求△HBC的面积.
考点:梯形
专题:
分析:延长BA与CD,两延长线交于点F,由CH垂直于BF,得到一对直角相等,由CH为角平分线得到一对角相等,再由CH为公共边,利用ASA可得出三角形CFH与三角形CBH全等,由全等三角形的对应边相等得到CF=CB,且BH=HF,由BH=3AH,得到HF=2AH,即A为HF的三等分点,由等腰三角形的两底角相等得到一对角相等,再由两直线平行得到一对同位角相等,等量代换并利用等角对等边得到三角形AFD为等腰三角形,且三角形AFD与三角形BFC相似,相似比为1:6,可得出面积之比为1:36,设三角形AFD的面积为x,则三角形BFC的面积为36x,可得出三角形EFC的面积为18x,再由四边形AHCD的面积为7,由四边形AHCD的面积+三角形AFD的面积等于三角形HFC的面积列出关于x的方程,求出方程的解得到x的值,18x即为所求.
解答: 解:延长BA,延长CD,两延长线交于点F,如图所示:
解:延长BA,延长CD,两延长线交于点F,如图所示:
∵CH⊥BF,
∴∠CHF=∠CHB=90°,
∵CH为∠BCD的平分线,
∴∠FCH=∠BCH,
在△FCH和△BCH中,
,
∴△FCH≌△BCH(ASA),
∴CF=CB,BH=FH,
∴∠F=∠B,
∵AD∥BC,
∴∠FAD=∠B,
∴∠F=∠FAD,
∴△AFD为等腰三角形,
又∵BE=3AH,
∴EF=3AH,即A为HF的三等分点,
∴△AFD∽△BFC,且相似比为1:6,
∴S△AFD:S△BFC=1:36,
设S△AFD=x,则S△BFC=36x,即S△HFC=18x,
由四边形AHCD的面积为21,得到S△HFC=x+21,
∴18x=x+21,
解得:x=
,
∴S△HBC=18x=
.
 解:延长BA,延长CD,两延长线交于点F,如图所示:
解:延长BA,延长CD,两延长线交于点F,如图所示:∵CH⊥BF,
∴∠CHF=∠CHB=90°,
∵CH为∠BCD的平分线,
∴∠FCH=∠BCH,
在△FCH和△BCH中,
|
∴△FCH≌△BCH(ASA),
∴CF=CB,BH=FH,
∴∠F=∠B,
∵AD∥BC,
∴∠FAD=∠B,
∴∠F=∠FAD,
∴△AFD为等腰三角形,
又∵BE=3AH,
∴EF=3AH,即A为HF的三等分点,
∴△AFD∽△BFC,且相似比为1:6,
∴S△AFD:S△BFC=1:36,
设S△AFD=x,则S△BFC=36x,即S△HFC=18x,
由四边形AHCD的面积为21,得到S△HFC=x+21,
∴18x=x+21,
解得:x=
| 21 |
| 17 |
∴S△HBC=18x=
| 378 |
| 17 |
点评:此题考查了等腰三角形的判定与性质,全等三角形的判定与性质,相似三角形的判定与性质,以及平行线的性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
下列条件中,不能判定△ABC≌△A1B1C1的是( )
| A、AB=A1B1,∠A=∠A1,AC=A1C1 |
| B、AB=A1B1,BC=B1C1,AC=A1C1 |
| C、AB=A1B1,∠B=∠B1,∠C=∠C1 |
| D、AC=A1C1,AB=A1B1,∠B=∠B1 |
 如图,已知⊙0的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则么∠P等于
如图,已知⊙0的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则么∠P等于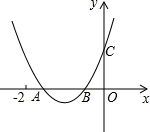 如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2-4ac<4a2;③a>
如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2-4ac<4a2;③a> 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是