题目内容
开口向下的抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),求m的值.
考点:二次函数的性质
专题:
分析:根据题意得出-
=-1,m2-2<0,进而求出m的值即可.
| 2m |
| 2(m2-2) |
解答:解:∵开口向下的抛物线y=(m2-2)x2+2mx+1的对称轴经过点(-1,3),
∴-
=-1,m2-2<0,
解得:m1=-1,m2=2(不合题意舍去),
∴m=-1.
∴-
| 2m |
| 2(m2-2) |
解得:m1=-1,m2=2(不合题意舍去),
∴m=-1.
点评:此题主要考查了二次函数的性质,根据题意得出关于m的值是解题关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
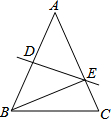 如图,将△ABC沿直线DE折叠,使得点A与点B重合,已知AC=8cm,△BCE的周长为13cm,则BC的长为( )
如图,将△ABC沿直线DE折叠,使得点A与点B重合,已知AC=8cm,△BCE的周长为13cm,则BC的长为( )| A、5cm | B、6cm |
| C、8cm | D、10cm |
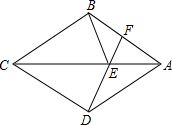 已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E. 已知:在梯形ABCD中,CD∥AB,AD=DC=BC=2,AB=4,∠B=60°.
已知:在梯形ABCD中,CD∥AB,AD=DC=BC=2,AB=4,∠B=60°. 已知:AC是?ABCD的对角线,且BE⊥AC,DF⊥AC.求证:四边形BFDE是平行四边形.
已知:AC是?ABCD的对角线,且BE⊥AC,DF⊥AC.求证:四边形BFDE是平行四边形.