题目内容
18.已知直线y=-$\frac{3}{2}$x+3和两坐标轴的交点为A,B,抛物线经过点A,B,且点(1,1)在此抛物线上,求此抛物线的顶点坐标和对称轴.分析 由直线的解析式求得A、B的坐标,进而根据待定系数法求得抛物线的解析式,然后把一般式化成顶点式即可.
解答 解:∵直线y=-$\frac{3}{2}$x+3和两坐标轴的交点为A,B,
∴A(2,0),B(0,3),
∵抛物线经过点A,B,且点(1,1)在此抛物线上,
∴设抛物线的解析式为y=ax2+bx+c,
则$\left\{\begin{array}{l}{4a+2b+c=0}\\{c=3}\\{a+b+c=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{5}{2}}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为;y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3,
∵y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3=$\frac{1}{2}$(x-$\frac{5}{2}$)2-$\frac{1}{8}$,
∴抛物线的顶点坐标为($\frac{5}{2}$,-$\frac{1}{8}$),对称轴为x=$\frac{5}{2}$.
点评 本题考查了待定系数法求二次函数的解析式以及二次函数的性质,把函数解析式整理顶点式形式求解更加简便.

练习册系列答案
相关题目
9.同一坐标系中作y=3x2,y=-3x2,y=$\frac{1}{3}$x2的图象,它们的共同特点是( )
| A. | 关于y轴对称,抛物线开口向上 | B. | 关于y轴对称,抛物线开口向下 | ||
| C. | 关于y轴对称,抛物线的顶点在原点 | D. | 关于x轴对称,抛物线的顶点在原点 |
 化简|a+b|+|a-c|-|b|+|b-c|.
化简|a+b|+|a-c|-|b|+|b-c|.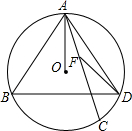 如图,△ABD内接于⊙O,AB=AD,点C在BD上,点F在AC上.
如图,△ABD内接于⊙O,AB=AD,点C在BD上,点F在AC上.