题目内容
若关于x的方程
=3+
无解,则m的值是( )
| x+1 |
| x-2 |
| m-1 |
| 2-x |
| A、-2 | B、2 | C、1 | D、-4 |
考点:分式方程的解
专题:
分析:先将分式方程化为整式方程,用含x的式子表示m的值,然后根据分式方程无实数根,得出x的值,继而求出m的值.
解答:解:
=3+
,
去分母得:x+1=3(x-2)-(m-1)
整理得:2x-m-6=0,
所以m=2x-6,
因为关于x的方程
=3+
无解,
所以x=2,
m=2×2-6=-2.
故选A.
| x+1 |
| x-2 |
| m-1 |
| 2-x |
去分母得:x+1=3(x-2)-(m-1)
整理得:2x-m-6=0,
所以m=2x-6,
因为关于x的方程
| x+1 |
| x-2 |
| m-1 |
| 2-x |
所以x=2,
m=2×2-6=-2.
故选A.
点评:本题考查分式方程的解,当无解时,就是有增根时,化成整式方程代入增根可求出m的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
现已知线段a,b(a<b),∠MON=90°,求作Rt△ABO,使得∠O=90°,AB=b,小惠和小雷的作法分别如下.
小惠:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点A为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点O为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是( )
小惠:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点A为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a为半径画弧,交射线ON于点A;②以点O为圆心、线段b长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是( )
| A、小惠的作法正确,小雷的作法错误 |
| B、小雷的作法正确,小惠的作法错误 |
| C、两人的作法都正确 |
| D、两人的作法都错误 |
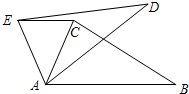 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A、30° | B、35° |
| C、40° | D、50° |
下列说法中不正确的是( )
| A、经过平移,图形对应点连成的线段平行且相等 |
| B、平移中,图形上每个点移动的距离不同 |
| C、经过平移,图形的对应线段,对应角分别相等 |
| D、平移不改变图形的形状和大小 |

 已知∠AOB=30°,点P在OA上,且OP=2,点P关于直线OB的对称点是Q,则PQ=
已知∠AOB=30°,点P在OA上,且OP=2,点P关于直线OB的对称点是Q,则PQ= 如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.
如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.