题目内容
16．
如图，?ABCD中，∠B=60°，AE⊥BC于B，AF⊥CD于F，BE=2，DF=3，求?ABCD的周长．
分析 在直角三角形ABE中求得AB的长，同理求得AD的长，继而求得平行四边形ABCD的周长．
解答 解：∵四边形ABCD是平行四边形，
∴∠B=∠D=60°，
∴∠BAE=∠FAD=30°，
∵AE⊥BC，AF⊥CD，
∵BE=2cm，FD=3cm，
∴AB=4cm，BC=AD=6cm，AF=3$\sqrt{3}$，
∴?ABCD的周长为=2（AB+BC）=20cm．
点评 此题考查了平行四边形的性质：平行四边形的对边平行且相等．还考查了直角三角形中30°角所对的直角边是斜边的一半，正确求得∠D的度数是关键．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
4．
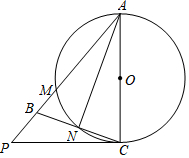如图，在△ABC中，AB=AC，以AC为直径的⊙O交与点M，交BC于点N，连接AN，过点C的切线交AB的延长线于点P．
（1）求证：∠BCD=∠BAN．
（2）若AC=4，PC=3，求MN•BC的值．
如图，在△ABC中，AB=AC，以AC为直径的⊙O交与点M，交BC于点N，连接AN，过点C的切线交AB的延长线于点P．（1）求证：∠BCD=∠BAN．
（2）若AC=4，PC=3，求MN•BC的值．
8．
如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD=2CD，点E，F分别为AB，AD的中点，则三角形AEF与多边形BCDFE的面积之比为（ ）
如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD=2CD，点E，F分别为AB，AD的中点，则三角形AEF与多边形BCDFE的面积之比为（ ）| A． | 1：7 | B． | 1：6 | C． | 1：5 | D． | 1：4 |