题目内容
已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G
不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,
将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
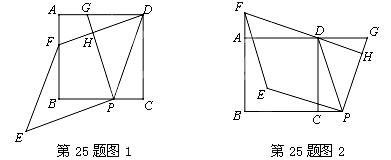
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD
是怎样的特殊四边形,并证明你的猜想.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 操作:
操作: 小英准备制作一个表面积为6cm2的正方体纸盒,现选用一些废弃的纸片进行如下设计:
小英准备制作一个表面积为6cm2的正方体纸盒,现选用一些废弃的纸片进行如下设计:
 | |||
 | |||

纸片利用率=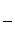 ×100%
×100%
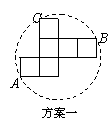
发现:(1) 小英发现方案一中的点A.B恰好为该圆一直径的两个端点.你认为
小英发现方案一中的点A.B恰好为该圆一直径的两个端点.你认为 小英的这个发现是否正确,请说明理由.
小英的这个发现是否正确,请说明理由.
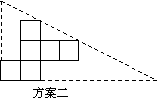
(2) 小英通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写
小英通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写 出求解过程.(结果精确到0.1%)
出求解过程.(结果精确到0.1%)
|
 小英感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.(结果精确到0.1%)
小英感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.(结果精确到0.1%) 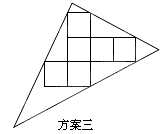
二次函数y=ax2+bx+c(a≠0)的部分对应值如下表:
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |
则二次函数y=ax2+bx+c在x=2时,y=___________.



 在河的两岸拉紧了一根细绳,并分别测出∠1=70°,∠2=70°,测出这个
在河的两岸拉紧了一根细绳,并分别测出∠1=70°,∠2=70°,测出这个
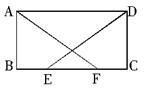
 =
= ,S△ABC=4,则四边形BCED的面积S四边形DB
,S△ABC=4,则四边形BCED的面积S四边形DB CE=
CE= 
 图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点
图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点 ,求tan∠EBC的值.
,求tan∠EBC的值.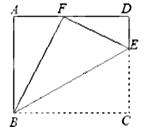
 ∥
∥ ,直线
,直线 与
与 C.65° D.125°
C.65° D.125°