题目内容
【题目】如图，矩形ABCD中，
，
，将矩形折叠，使点B与点D重合，点A的对应点为
，折痕EF的长为________.
【答案】
【解析】
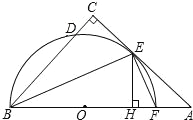
过点F作FH⊥AD于H，先利用矩形的性质及轴对称的性质证明DE=DF=BF，在Rt△DCF中通过勾股定理求出DF的长，再求出HE的长，再在Rt△HFE中利用勾股定理即可求出EF的长．
解：如图，过点F作FH⊥AD于H，
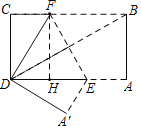
∵四边形ABCD为矩形，
∴BC∥AD，∠C=90°，DC=AB=4，四边形DCFH为矩形，
∴∠BFE=∠DEF，
由折叠可知，∠BFE=∠DFE，BF=DF，
∴∠DEF=∠DFE，
∴DE=DF=BF，
在Rt△DCF中
设DF=x，则CF=BC-BF=6-x，
∵DC2+CF2=DF2，
∴42+（6-x）2=x2，
解得，x=
，
∴DE=DF=BF=，
∴CF=BC-BF=6-=
，
∵四边形DCFH为矩形，
∴HF=CD=4，DH=CF=，
∴HE=DE-DH=
，
∴在Rt△HFE中，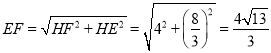
故答案为
练习册系列答案
相关题目
