题目内容
 如图,
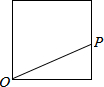
如图,(1)已知AD与BC相交于点O,∠BAD的平分线AE与∠BCD的平分线CE相交于点E,AB∥CD,∠D=40°,∠B=30°,求∠E的度数.
(2)已知AD与BC相交于点O,∠BAD的平分线AE与∠BCD的平分线CE相交于点E,∠B=m°,∠D=n°.
①求∠E的度数(用含m°、n°的式子表示);
②当∠B:∠D:∠E=3:5:x时,求x的值.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线的定义,得出∠ECD=∠ECB=
∠BCD,∠EAD=∠EAB=
∠BAD,根据∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,从而求得∠D+∠B=2∠E,得出∠E=
(∠D+∠B),从而得解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=
∠BCD,∠EAD=∠EAB=
∠BAD,
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E.
∵∠D=40°,∠B=30°,
∴∠E=
(∠D+∠B)=35°;
(2)①∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=
∠BCD,∠EAD=∠EAB=
∠BAD,
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E.
∵∠B=m°,∠D=n°.
∴∠E=
(m°+n°);
②∵∠E=
(∠D+∠B),∠B:∠D:∠E=3:5:x,
∴x=
(3+5)=4,
∴∠ECD=∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E.
∵∠D=40°,∠B=30°,
∴∠E=
| 1 |
| 2 |
(2)①∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E.
∵∠B=m°,∠D=n°.
∴∠E=
| 1 |
| 2 |
②∵∠E=
| 1 |
| 2 |
∴x=
| 1 |
| 2 |
点评:考查了平行线的性质,三角形内角和定理,对顶角相等的性质,熟练掌握性质和定理是解题的关键.

练习册系列答案
相关题目
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
下列说法正确的个数有( )
①|a|一定是正数;②-a一定是负数;③-(-a)一定是正数;④
一定是分数.
①|a|一定是正数;②-a一定是负数;③-(-a)一定是正数;④
| a |
| 7 |
| A、0个 | B、1个 | C、2个 | D、3个 |
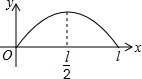 点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )
点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )