题目内容
 如图在Rt△ABC中,∠C=90°,AC=8,BC=6,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,当其中一点到达端点时,另一点也随之停止运动.连结PQ,M为线段PQ的中点,则在整个运动过程中,M点所经过的路径长为
如图在Rt△ABC中,∠C=90°,AC=8,BC=6,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,当其中一点到达端点时,另一点也随之停止运动.连结PQ,M为线段PQ的中点,则在整个运动过程中,M点所经过的路径长为考点:轨迹
专题:压轴题
分析:先以C为原点,以AC所在直线为x轴,建立平面直角坐标系,由题意知0≤t≤3,求得t=0及t=3时M的坐标,得到直线M1M2的解析式为y=-2x+8.过点M2作M2N⊥x轴于点N,则M2N=3,M1N=
,M1M2=
,线段PQ中点M所经过的路径长为
个单位长度.
| 3 |
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
解答:解:以C为原点,以AC所在直线为x轴,建立平面直角坐标系,

依题意,可知0≤t≤3,当t=0时,点M1的坐标为(4,0);
当t=3时,点M2的坐标为(
,3),设直线M1M2的解析式为y=kx+b,
∴
,
解得:
,
∴直线M1M2的解析式为y=-2x+8.
∵点Q(0,2t),P(8-t,0),
∴在运动过程中,线段PQ中点M3的坐标为(
,t),
把x=
,代入y=-2x+8,得y=-2×
+8=t,
∴点M3在M1M2直线上,
过点M2作M2N⊥x轴于点N,则M2N=3,M1N=
,
∴M1M2=
,
∴线段PQ中点M所经过的路径长为
单位长度.
故答案为:
.

依题意,可知0≤t≤3,当t=0时,点M1的坐标为(4,0);
当t=3时,点M2的坐标为(
| 5 |
| 2 |
∴
|
解得:
|
∴直线M1M2的解析式为y=-2x+8.
∵点Q(0,2t),P(8-t,0),
∴在运动过程中,线段PQ中点M3的坐标为(
| 8-t |
| 2 |
把x=
| 6-t |
| 2 |
| 8-t |
| 2 |
∴点M3在M1M2直线上,
过点M2作M2N⊥x轴于点N,则M2N=3,M1N=
| 3 |
| 2 |
∴M1M2=
3
| ||
| 2 |
∴线段PQ中点M所经过的路径长为
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |
点评:本题主要考查了一次函数的应用.用到解二元一次方程组以及勾股定理,综合性较强.

练习册系列答案
相关题目
已知反比例函数y=
的图象经过点(2,-4),则k的值为( )
| k |
| x |
| A、4 | ||
B、-
| ||
| C、-4 | ||
| D、-8 |
 如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC,OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点Q在线 段OC上由C向点O运动,QD⊥OC交 直线BC于点D,当一个点到达终点时,另一个点也停止运动.
如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC,OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点Q在线 段OC上由C向点O运动,QD⊥OC交 直线BC于点D,当一个点到达终点时,另一个点也停止运动. 如图,一个正六边形转盘被分成6个全等的正三角形,任意旋转这个转盘1次,当旋转停止时,指针指向阴影区域的概率是
如图,一个正六边形转盘被分成6个全等的正三角形,任意旋转这个转盘1次,当旋转停止时,指针指向阴影区域的概率是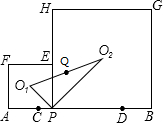 如图:已知AB=10,点C、D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形APEF和正方形PBGH,点O1和O2是这两个正方形的中心,连接O1O2,设O1O2的中点为Q;当点P从点C运动到点D时,则点Q移动路径的长是
如图:已知AB=10,点C、D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形APEF和正方形PBGH,点O1和O2是这两个正方形的中心,连接O1O2,设O1O2的中点为Q;当点P从点C运动到点D时,则点Q移动路径的长是