题目内容
先化简,再求值
(1)(a+b)2+(a-b)(2a+b)-3a2,其中a=-2,b=b=
;
(2)(4a3b-8a2b2)÷ab-(2a+b)(2a-b),其中a=-
,b=1.
(1)(a+b)2+(a-b)(2a+b)-3a2,其中a=-2,b=b=
| 1 |
| 2 |
(2)(4a3b-8a2b2)÷ab-(2a+b)(2a-b),其中a=-
| 1 |
| 2 |
考点:整式的混合运算—化简求值
专题:
分析:(1)先利用完全平方公式和多项式乘多项式的方法计算,再合并同类项,再进一步代入求得数值即可;
(2)利用平方差公式和整式的除法计算,再进一步合并同类项,最后代入求得数值即可.
(2)利用平方差公式和整式的除法计算,再进一步合并同类项,最后代入求得数值即可.
解答:解:(1)(a+b)2+(a-b)(2a+b)-3a2
=a2+2ab+b2+2+2a2-ab-b2-3a2
=ab-b2
当a=-2,b=
时
原式=(-2)×
-(
)2
=-1-
=-
;
(2)(4a3b-8a2b2)÷ab-(2a+b) (2a-b)
=4a2-4ab-(4a2-b2)
=4a2-8ab-4a2+b2
=-8ab+b2
当a=-
,b=1时
原式=-8×(-
)×1+12=5.
=a2+2ab+b2+2+2a2-ab-b2-3a2
=ab-b2
当a=-2,b=
| 1 |
| 2 |
原式=(-2)×
| 1 |
| 2 |
| 1 |
| 2 |
=-1-
| 1 |
| 4 |
=-
| 5 |
| 4 |
(2)(4a3b-8a2b2)÷ab-(2a+b) (2a-b)
=4a2-4ab-(4a2-b2)
=4a2-8ab-4a2+b2
=-8ab+b2
当a=-
| 1 |
| 2 |
原式=-8×(-
| 1 |
| 2 |
点评:此题考查整式的化简求值,注意灵活运用公式计算,代入注意字母与数值的对应.

练习册系列答案
相关题目
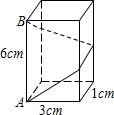 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要( )
如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要( )| A、8cm | B、10cm |
| C、12cm | D、15cm |
使代数式
有意义的x的取值范围是( )
| ||
| 2x-6 |
| A、x≠3 |
| B、x<5且x≠3 |
| C、x≤5且x≠2 |
| D、x≤5且x≠3 |
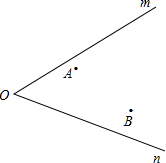 电信部门要建一座发射塔,如图:按照设计要求,发射塔建在高速公路m和n所夹右侧区域且到城镇A、B距离相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?请标出它的位置.(保留作图痕迹)
电信部门要建一座发射塔,如图:按照设计要求,发射塔建在高速公路m和n所夹右侧区域且到城镇A、B距离相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?请标出它的位置.(保留作图痕迹)