题目内容
①式子4-a2-2ab-b2的最大值是________．
②已知
，则
=________．
4 527
分析：①逆运用完全平方公式整理，然后即可求解；
②利用完全平方公式把已知条件两边平方然后再整理即可得解．
解答：①4-a2-2ab-b2=4-（a2+2ab+b2）=4-（a+b）2，
∵（a+b）2≥0，
∴-（a+b）2≤0，
∴当式子（a+b）2=0时，式子4-a2-2ab-b2的最大值是4；
②∵
-
=5，
∴（-）2=25，
即
-2×
+
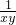=25，
∵xy=-1，
∴+=25+2÷（-1）=23，
∴（+）2=232，
即
+2×
+
=529，
∴+=529-2÷（-1）2=527．
故答案为：4；527．
点评：本题考查了完全平方公式，熟记公式是解题的关键．完全平方公式：（a±b）2=a2±2ab+b2．
分析：①逆运用完全平方公式整理，然后即可求解；
②利用完全平方公式把已知条件两边平方然后再整理即可得解．
解答：①4-a2-2ab-b2=4-（a2+2ab+b2）=4-（a+b）2，
∵（a+b）2≥0，
∴-（a+b）2≤0，
∴当式子（a+b）2=0时，式子4-a2-2ab-b2的最大值是4；
②∵
-=5，∴（
-）2=25，即
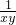-2×+=25，∵xy=-1，
∴
+=25+2÷（-1）=23，∴（
+）2=232，即
+2×+=529，∴
+=529-2÷（-1）2=527．故答案为：4；527．
点评：本题考查了完全平方公式，熟记公式是解题的关键．完全平方公式：（a±b）2=a2±2ab+b2．
练习册系列答案
相关题目
式子
=1-a成立，则a的取范围是（ ）
| a2-2a+1 |
| A、a＞1 | B、a＜1 |
| C、a≥1 | D、a≤1 |
如图，梯形的上底为a2+2a-10，下底为3a2-5a-80，高为40．（π取3）