题目内容
18.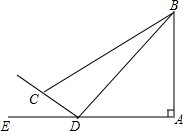 如图所示,某学校教学活动小组欲测量一颗大树AB的高度,他们在斜坡上C处测得大树顶端B的仰角是30°,朝大树方向沿斜坡向下走6m到达坡脚D处,在D处测得大树顶端B的仰角是45°,若斜坡CD的坡比i=1:$\sqrt{3}$,求大树的高度AB.(结果精确到0.1m,参考数据:$\sqrt{2}≈1.41,\sqrt{3}≈1.73$)
如图所示,某学校教学活动小组欲测量一颗大树AB的高度,他们在斜坡上C处测得大树顶端B的仰角是30°,朝大树方向沿斜坡向下走6m到达坡脚D处,在D处测得大树顶端B的仰角是45°,若斜坡CD的坡比i=1:$\sqrt{3}$,求大树的高度AB.(结果精确到0.1m,参考数据:$\sqrt{2}≈1.41,\sqrt{3}≈1.73$)
分析 过点C分别作CF⊥DE,CG⊥AB,垂足分别为F、G,由已知条件得到CF=3,DF=3$\sqrt{3}$,设AD=xm,得到AB=AD=x,BG=x-3,AF=x+3$\sqrt{3}$,根据三角函数的定义列方程即可得到结论.
解答 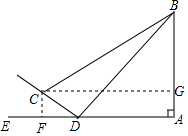 解:过点C分别做CF⊥DE,CG⊥AB,垂足分别为F、G,
解:过点C分别做CF⊥DE,CG⊥AB,垂足分别为F、G,
∵i=1+$\sqrt{3}$,CD=6,
∴CF=3,DF=3$\sqrt{3}$,
设AD=xm,
∵∠ADB=45°,
∴AB=AD=x.
∴BG=x-3,AF=x+3$\sqrt{3}$,
∴CG=$\sqrt{3}$,
在Rt△BCG中,∠BCG=30°,
∴tan∠BCG=$\frac{BG}{CG}=\frac{\sqrt{3}}{3}$,
即$\frac{x-3}{x+3\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴x≈14.2m.
答:大树AB的高度约为14.2m.
点评 本题考查了仰角、坡角的定义,解直角三角形的应用,能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
6.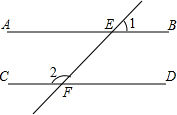 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )| A. | 44° | B. | 46° | C. | 134° | D. | 144° |
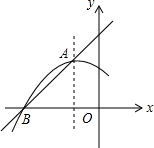 如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点A的坐标为(-1,2),与x轴的一个交点B的坐标为(-3,0),直线y2=mx+n与抛物线交于A、B两点.下列结论:①2a-b=0;②abc<0;③a+b+c=0;④方程ax2+bx+c=5没有实数根;⑤当y1<y2时,x>-1.其中正确的是( )
如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点A的坐标为(-1,2),与x轴的一个交点B的坐标为(-3,0),直线y2=mx+n与抛物线交于A、B两点.下列结论:①2a-b=0;②abc<0;③a+b+c=0;④方程ax2+bx+c=5没有实数根;⑤当y1<y2时,x>-1.其中正确的是( )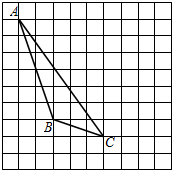 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′,利用网格点和直尺画图.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′,利用网格点和直尺画图.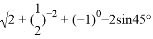
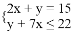 的x、y的正整数解。
的x、y的正整数解。