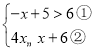Question

【题目】已知：关于x的方程x2+（m-2）x+m-3=0．
（1）求证：无论m取什么实数，这个方程总有两个不相等的实数根；
（2）若这个方程的两个实数根x1，x2满足2x1+x2=m+1，求m的值．

Answer 1

【答案】（1）详见解析；（2）0，

【解析】

（1）△=（m-2）2-4×（m-3）=（m-3）2+7＞0，无论m取什么实数，这个方程总有两个不相等的实数根；（2）根据根与系数关系可得：（2m-1）2+（m-2）（2m-1）+m-3=0.

（1）证明：△=（m-2）2-4×（m-3），
=m2-6m+16，
=（m-3）2+7＞0，
∴无论m取什么实数，这个方程总有两个不相等的实数根；
（2）x1+x2=-（m-2），
2x1+x2=x1+（x1+x2）=m+1，
∴x1=m+1+m-2=2m-1，
把x1代入方程有：
（2m-1）2+（m-2）（2m-1）+m-3=0，
整理得：
6m2-m=0，
6m（m-）=0，
∴m1=0，m2=．