��Ŀ����
����Ŀ��ij�о�����ˮʵ���Ի�Ϊ��λ�����������շѰ취��
��һ��������ÿ��ÿ����ˮ![]() �����ں�
�����ں�![]() �֣�ÿ����ˮ��
�֣�ÿ����ˮ��![]() Ԫ��
Ԫ��
�ڶ���������ÿ��ÿ����ˮ����![]() �ֵ�������
�ֵ�������![]() �֣�δ����
�֣�δ����![]() �IJ��ְ��յ�һ�����շѣ���������ÿ����ˮ��
�IJ��ְ��յ�һ�����շѣ���������ÿ����ˮ��![]() Ԫ��
Ԫ��
������������ÿ��ÿ����ˮ����![]() �֣�δ����
�֣�δ����![]() �ֵIJ��ְ��յ�һ���������շѣ���������ÿ����ˮ��
�ֵIJ��ְ��յ�һ���������շѣ���������ÿ����ˮ��![]() Ԫ��
Ԫ��
��һ����������ˮ![]() �֣�Ӧ��ˮ��
�֣�Ӧ��ˮ��![]() Ԫ��
Ԫ��![]() ��
��![]() ֮��ĺ�����ϵ��ͼ��ʾ��
֮��ĺ�����ϵ��ͼ��ʾ��
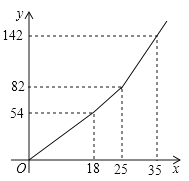
������ͼ��ֱ������![]() ___________��
___________��![]() _______________��
_______________��![]() _______________��
_______________��
������![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��������ˮ�ѽ����շѰ취��Ϊ�����٣����軹���ڷ����ڣ�����ÿ������ˮһ�ɰ���ÿ��![]() Ԫ�ı��ɷ�.�������û�����ˮ����
Ԫ�ı��ɷ�.�������û�����ˮ����![]() ��ʱ��������ݾ���ÿ������ˮ���Ĵ�С��Ƴ��Ծ���ɷ���ʵ�ݵķ���.
��ʱ��������ݾ���ÿ������ˮ���Ĵ�С��Ƴ��Ծ���ɷ���ʵ�ݵķ���.
���𰸡�����![]() ������
������![]() ������
������![]() ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���
ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���![]() ʱ��ѡ�����ֽɷѷ���������ͬ����
ʱ��ѡ�����ֽɷѷ���������ͬ����![]() ʱ��ѡ��ɷѷ����ڸ�ʵ��.
ʱ��ѡ��ɷѷ����ڸ�ʵ��.
��������
��1�����ݵ���=�ܼ����������������a��b��c��ֵ��
��2���۲캯��ͼ���ҳ�������꣬���ô���ϵ�������������x��25ʱy��x֮��ĺ�����ϵ��
��3�����ܼ�=�������������ҳ�ѡ��ɷѷ������轻ˮ��y��Ԫ������ˮ����x���֣�֮��ĺ�����ϵʽ���ֱ��ҳ���6x-68��4x��6x-68=4x��6x-68��4xʱx��ȡֵ��Χ��x��ֵ����ѡ����õ͵ķ������ɵó����ۣ�
�⣺����a=54��18=3��
b=��82-54������25-18��=4��
c=��142-82������35-25��=6��
�ʴ�Ϊ��3,��4��6��
�����赱x��25ʱ��y��x֮��ĺ�����ϵʽΪy=mx+n��m��0����
����25��82������35��142������y=mx+n���ã�![]() ��
��
��ã�![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() .
.
����ѡ��ɷѷ������轻ˮ��![]() ��Ԫ������ˮ��
��Ԫ������ˮ��![]() ���֣�֮��ĺ�����ϵʽΪ
���֣�֮��ĺ�����ϵʽΪ![]() .
.
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() .
.
�൱![]() ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���
ʱ��ѡ��ɷѷ����ٸ�ʵ�ݣ���![]() ʱ��ѡ�����ֽɷѷ���������ͬ����
ʱ��ѡ�����ֽɷѷ���������ͬ����![]() ʱ��ѡ��ɷѷ����ڸ�ʵ��.
ʱ��ѡ��ɷѷ����ڸ�ʵ��.

����Ŀ��ѧУ�˶����������Զ��1���������������������ֳ�Ԥ���;��������Σ��±�Ϊ�μ������������10��ѧ����Ԥ���ɼ���
ѧ����� �ɼ� ��Ŀ | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
������Զ����λ���ף� | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1��������������� | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
����10��ѧ���У�ͬʱ�������������ֻ��6�ˣ�����������Զ��������8![]() ��ֵ��__________��
��ֵ��__________��