题目内容
7．a、b、c取什么数值时，x3-ax2+bx+c与（x-1）（x-2）（x-3）恒等？分析 根据多项式乘以多项式的法则，可表示为（a+b）（m+n）=am+an+bm+bn，计算即可．
解答 解：（x-1）（x-2）（x-3）
=（x2-3x+2）（x-3），
=x3-6x2+11x-6，
因为x3-ax2+bx+c与（x-1）（x-2）（x-3）相等，
所以可得：a=6，b=11，c=-6．
故当a=6，b=11，c=-6时，x3-ax2+bx+c与（x-1）（x-2）（x-3）恒等．
点评 本题主要考查多项式乘以多项式的法则．注意不要漏项，漏字母，有同类项的合并同类项．
练习册系列答案
相关题目
18．若一个多边形的每个内角都等于150°，则这个多边形的边数是（ ）
| A． | 10 | B． | 11 | C． | 12 | D． | 13 |
15．
如图，是抛物线y=ax2+bx+c（a≠0）图象的一部分．已知抛物线的对称轴为x=2，它与x轴的一个交点是（-1，0）．则抛物线与x轴的另一个交点是（5，0）；a+b+c＜0（填“＜或=或＞”）
如图，是抛物线y=ax2+bx+c（a≠0）图象的一部分．已知抛物线的对称轴为x=2，它与x轴的一个交点是（-1，0）．则抛物线与x轴的另一个交点是（5，0）；a+b+c＜0（填“＜或=或＞”）
2．
如图，有一个工件，它的左视图是（ ）
如图，有一个工件，它的左视图是（ ）| A． |  | B． |  | C． |  | D． |  |
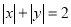,下图画出了符合条件的点P所组成图形的一部分，请将所有符合条件的点P所组成的图形补充完整.