题目内容
5.我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的腰长为2,“内角正度值”为45°,那么该三角形的面积等于2或1.分析 根据新定理,设最小角为x,则最大角为x+45°,再分类讨论:当顶点为x+45°时,根据三角形内角和可求得x=45°,则可判断此三角形为等腰直角三角形,易得此三角形的面积=2;当顶点为x时,根据三角形内角和定理可求得x=30°,所以此三角形为顶点为30度的等腰三角形,如图,AB=AC=2,∠A=30°,作CD⊥AB于D,在Rt△ADC中,利用∠A=30°可得CD=$\frac{1}{2}$AC=1,则根据三角形面积公式计算出三角形ABC的面积=$\frac{1}{2}$CD•AB=1,综上所述,该三角形的面积等于1或2.
解答 解:设最小角为x,则最大角为x+45°,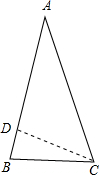
当顶点为x+45°时,则x+x+x+45°=180°,解得x=45°,所以此三角形为等腰直角三角形,此三角形的面积=$\frac{1}{2}$×2×2=2;
当顶点为x时,则x+x+45°+x+45°=180°,解得x=30°,所以此三角形为顶点为30度的等腰三角形,如图,AB=AC=2,∠A=30°,
作CD⊥AB于D,在Rt△ADC中,∵∠A=30°,
∴CD=$\frac{1}{2}$AC=1,
∴三角形ABC的面积=$\frac{1}{2}$CD•AB=$\frac{1}{2}$×1×2=1,
综上所述,该三角形的面积等于1或2.
故答案为1或2.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了等腰三角形的性质.

练习册系列答案
相关题目
16.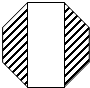 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )| A. | $10\sqrt{2}$ | B. | 20 | C. | 18 | D. | $20\sqrt{2}$ |
13.将抛物线y=x2向下平移1个单位,再向左平移2个单位后,所得新抛物线的表达式是( )
| A. | y=(x-1)2+2 | B. | y=(x-2)2+1 | C. | y=(x+1)2-2 | D. | y=(x+2)2-1 |
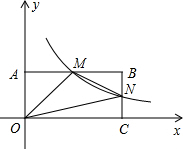 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(6,3),直线y=-$\frac{1}{2}$x+4交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(6,3),直线y=-$\frac{1}{2}$x+4交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.