题目内容
10．已知p是实数，若a，b是关于x的一元二次方程x2-2x+p-1=0的两个非负实根，则（a-1）（b-1）的最小值是（ ）| A． | -2 | B． | -3 | C． | 0 | D． | -1 |
分析 根据方程根的判别式，可得p的取值范围，根据根与系数的关系，可得ab，（a+b）的值，根据p的取值范围，可得答案．
解答 解：由x的一元二次方程x2-2x+p-1=0的两个非负实根，得$\left\{\begin{array}{l}{△=（-2）^{2}-4（p-1）≥0}\\{\frac{2-\sqrt{（-2）^{2}-4（p-1）}}{2}≥0}\end{array}\right.$，
解得1≤p≤2，
a+b=2，ab=p-1．
（a-1）（b-1）=-（a+b）+ab+1=-2+p-1+1
当p=1时，a-1）（b-1）=-2+1-1+1=-1，
故选：D．
点评 本题考查了根与系数的关系，利用根的判别式、根是非负数得出不等式组是解题关键，又利用了根与系数的关系．
练习册系列答案
相关题目
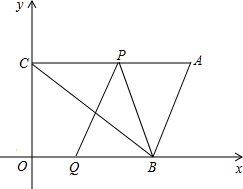如图，B（16，0），C（0，12），AC∥x轴，AC=21，动点P从点C出发，沿射线CA的方向以每秒2个长度单位的速度运动，动点Q从点O出发，在线OB上以每秒1个长度单位的速度向点B运动，点P，Q分别从点C，O同时出，当点Q运动到点B时，点P随之停止运动，设运动时间为t（秒）．