题目内容
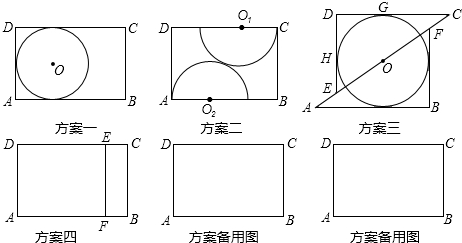
19.木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:方案一:直接锯一个半径最大的圆;
方案二:圆心O1、O2分别在CD、AB上,半径分别是O1C、O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
方案四:锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的圆.
(1)写出方案一中圆的半径.
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE=x(0<x<1),当x取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大.
分析 (1)直接利用CB的长即可得出圆的半径长;
(2)分别利用勾股定理以及相似三角形的判定与性质得出两半径长进而得出答案;
(3)首先得出所截出圆的直径最大为(3-x)或(2+x)两者之中较小的一个再利用一次函数增减性得出即可.
解答 解:(1)方案一中的最大半径为1;
(2)设半径为r,
方案二:如图方案二,连接O1O2,O1E,在Rt△O1O2E中,(2r)2=22+(3-2r)2,
解得 r=$\frac{13}{12}$,
方案三:如图方案三,连接ON,OM,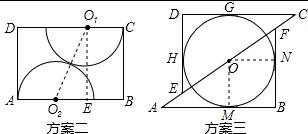
∵ON∥AM,
∴∠FON=∠A,
又∵∠ONF=∠AMO=90°,
∴△AOM∽△OFN,
∴$\frac{ON}{AM}$=$\frac{FN}{MO}$,
∴$\frac{r}{3-r}$=$\frac{2-r}{r}$,
解得:r=$\frac{6}{5}$,
∵$\frac{13}{12}$<$\frac{6}{5}$,
∴方案三半径较大;
(3)方案四所拼得的图形水平方向跨度为3-x,竖直方向跨度为2+x.
所以所截出圆的直径最大为(3-x)或(2+x)两者之中较小的.
当3-x<2+x时,即当x>$\frac{1}{2}$时,r=$\frac{1}{2}$(3-x);
此时r随x的增大而减小,所以r<$\frac{1}{2}$(3-$\frac{1}{2}$)=$\frac{5}{4}$;
当3-x=2+x时,即当x=$\frac{1}{2}$时,r=$\frac{1}{2}$ (3-$\frac{1}{2}$)=$\frac{5}{4}$;
当3-x>2+x时,即当x<$\frac{1}{2}$时,r=$\frac{1}{2}$ (2+x).
此时r随x的增大而增大,所以r<$\frac{1}{2}$ (2+$\frac{1}{2}$)=$\frac{5}{4}$;
∴方案四,当x=$\frac{1}{2}$时,r最大为$\frac{5}{4}$,
∵1<$\frac{13}{12}$$<\frac{6}{5}$<$\frac{5}{4}$,
∴方案四中所得到的圆形桌面的半径最大.
点评 此题主要考查了圆的综合以及相似三角形的判定与性质和一次函数的增减性等知识,利用分类讨论得出r的最值是解题关键.

| A. | 65和60 | B. | 65和55 | C. | 94和60 | D. | 94和55 |
| A. | 77×105 | B. | 7.7×106 | C. | 7.7×105 | D. | 0.77×106 |
| A. | 36 | B. | 38 | C. | 34 | D. | 28 |
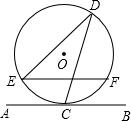 如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )
如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )| A. | 2$\sqrt{3}$ | B. | 8 | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{13}$ |
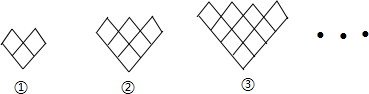
 如图是用棋子摆成的“T”字图案.从图案中可以看出,第1个“T”字型图案需要5枚棋子,第2个“T”字型图案需要8枚棋子,第3个“T”字型图案需要11枚棋子.
如图是用棋子摆成的“T”字图案.从图案中可以看出,第1个“T”字型图案需要5枚棋子,第2个“T”字型图案需要8枚棋子,第3个“T”字型图案需要11枚棋子.