题目内容
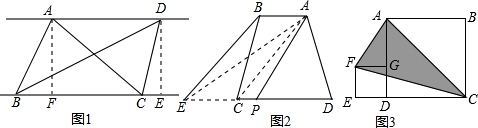
7.(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD.证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC=$\frac{1}{2}$×BC×AF,S△BCD=$\frac{1}{2}×BC×DE$.
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样.同底等高的两三角形面积相等
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:S?ABCD=S△APD
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2,则图中阴影三角形的面积是40cm2.
分析 (1)根据两三角形的特殊性同底等高得出结论;
(2)根据等底等高可得S△ABC=S△AEC,即可证明S梯形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED;
(3)根据面积的和差得到阴影部分(△ACF)的面积=$\frac{1}{2}$S正方形ABCD.
解答 解;(1)利用图形直接得出:同底等高的两三角形面积相等;
故答案为:同底等高的两三角形面积相等;
(2)∵AB∥CE,BE∥AC,
∴四边形ABEC为平行四边形,
∴△ABC和△AEC的公共边AC上的高也相等,
∴S△ABC=S△AEC,
∴S梯形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED;
(3)设正方形ABCD的边长为a,正方形DGFE的边长为b,
∵S△ACF=S四边形ACEF-S△CEF=S△AFG+S正方形DEFG+S△ADC-S△CEF=$\frac{1}{2}$×b×(a-b)+b×b+$\frac{1}{2}$×a×a-$\frac{1}{2}$×b×(b+a)=$\frac{1}{2}$ab-$\frac{1}{2}$b2+b2+$\frac{1}{2}$a2-$\frac{1}{2}$b2-$\frac{1}{2}$ab=$\frac{1}{2}$a2,
∴S△ACF=$\frac{1}{2}$S正方形ABCD=$\frac{1}{2}$×80cm2=40cm2;
故答案为:40.
点评 本题考查了学生的阅读理解能力,以及运用三角形、等底等高性质等基础知识解决问题的能力都有较高的要求.还渗透了由“特殊”到“一般”的数学思想.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
12.下列运算中正确的是( )
| A. | 2a-a=2 | B. | a2+a3=a5 | C. | ab2÷a=b2 | D. | (-2a)3=-6a3 |
16.观察一列数据:1,-2,3,-4,5,-6,…,根据你所发现的规律,则第2015个数是( )
| A. | -2015 | B. | 2015 | C. | -2014 | D. | 2016 |
17.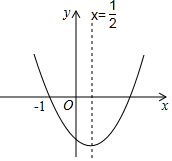 抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )
抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )
 抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )
抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )| A. | x1=-1,x2=$\frac{1}{2}$ | B. | x1=-1,x2=0 | C. | x1=-1,x2=2 | D. | x1=-1,x2=$\frac{3}{2}$ |

 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+4与x轴、y轴分别交于点A、B,直线CD与y轴交于点C(0,-8),与直线AB交于点D,若△AOB∽△CDB,则点D的坐标为($\frac{24}{5}$,$\frac{8}{5}$).
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+4与x轴、y轴分别交于点A、B,直线CD与y轴交于点C(0,-8),与直线AB交于点D,若△AOB∽△CDB,则点D的坐标为($\frac{24}{5}$,$\frac{8}{5}$).