题目内容
 如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=144cm2,DE长是( )
如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=144cm2,DE长是( )| A、4.6cm | B、4.8cm |
| C、5cm | D、无法确定 |
考点:角平分线的性质
专题:
分析:根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离都等于DE的长度,然后根据△ABC的面积列方程求解即可.
解答:解:∵BD是∠ABC平分线,DE⊥AB,
∴点D到AB、BC的距离都等于DE的长度,
∴S△ABC=
(AB+BC)•DE=144,
即
(36+24)•DE=144,
解得DE=4.8cm.
故选B.
∴点D到AB、BC的距离都等于DE的长度,
∴S△ABC=
| 1 |
| 2 |
即
| 1 |
| 2 |
解得DE=4.8cm.
故选B.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质并根据三角形的面积列出方程是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
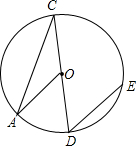 如图,CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠A的度数为( )
如图,CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠A的度数为( )| A、50° | B、40° |
| C、30° | D、25° |
若方程3x+5=17的解也是关于x的方程
-a=4的解,则a的值为( )
| x |
| 2 |
| A、-6 | B、2 | C、16 | D、-2 |
下列五种说法:①一个数的绝对值不可能是负数;②不带根号的数一定是有理数;③负数没有立方根;④-
是17的平方根;⑤两个无理数的和一定是无理数或零,其中正确的说法有( )
| 17 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列方程中,属于一元二次方程的是( )
| A、x+2y=5 | ||
| B、x2+y=3 | ||
C、3x=
| ||
D、x+
|
 如图,∠A=30°,∠B′=62°,△ABC与△A′B′C′关于直线l对称,则△ABC中的∠C=
如图,∠A=30°,∠B′=62°,△ABC与△A′B′C′关于直线l对称,则△ABC中的∠C= 如图,已知过A、C、D三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=57°,那么∠ABC=
如图,已知过A、C、D三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=57°,那么∠ABC=