题目内容
15.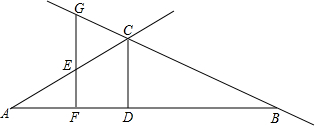 如图,已知CD⊥AB于D,E是射线AC上一动点,EF⊥AB于F,EF交直线BC于G,若∠AEF=∠CGE.
如图,已知CD⊥AB于D,E是射线AC上一动点,EF⊥AB于F,EF交直线BC于G,若∠AEF=∠CGE.(1)求证:CD平分∠ACB,下面给出了部分证明过程和理由,请你补充完善:
证明:∵CD⊥AB,EF⊥AB(已知)
∴∠ADC=∠AFE=90°(垂直的定义)
∴CD∥FG(同位角相等,两直线平行)
∴∠ACD=∠AEF(两直线平行,同位角相等)
∠BCD=∠CGE(两直线平行,内错角相等)
∵∠AEF=∠CGE(已知)
∴∠ACD=∠BCD即CD平分∠ACB(角平分线的定义)
(2)将EF向右平移,使点E在AC的延长线上,(1)中的结论是否还成立?若成立,请画出图形;若不成立,请画出图形,写出正确结论.
分析 (1)根据CD⊥AB,EF⊥AB,即可得到CD∥FG,根据平行线的性质,即可得到∠ACD=∠AEF,∠BCD=∠CGE,再根据∠AEF=∠CGE,即可得出∠ACD=∠BCD,进而得到CD平分∠ACB;
(2)根据使点E在AC的延长线上,EF⊥AB于F,EF交直线BC于G,即可画出图形.
解答 解:(1)∵CD⊥AB,EF⊥AB(已知)
∴∠ADC=∠AFE=90°(垂直的定义)
∴CD∥FG(同位角相等,两直线平行)
∴∠ACD=∠AEF(两直线平行,同位角相等)
∠BCD=∠CGE(两直线平行,内错角相等)
∵∠AEF=∠CGE(已知)
∴∠ACD=∠BCD,即CD平分∠ACB(角平分线的定义)
故答案为:垂直的定义;FG,同位角相等,两直线平行;∠AEF;∠CGE,两直线平行,同位角相等;角平分线的定义;
(2)成立.如图所示:
理由:∵CD⊥AB,EF⊥AB(已知)
∴∠ADC=∠AFE=90°(垂直的定义)
∴CD∥FG(同位角相等,两直线平行)
∴∠ACD=∠AEF(两直线平行,同位角相等)
∠BCD=∠CGE(两直线平行,内错角相等)
∵∠AEF=∠CGE(已知)
∴∠ACD=∠BCD,即CD平分∠ACB(角平分线的定义)
点评 本题主要考查了平行线的性质与判定的运用,解题时注意:两直线平行,同位角相等;两直线平行,内错角相等.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
7.星期天上午,某动物园熊猫馆来了甲、乙两队游客,两队游客的年龄如表所示:
甲队
乙队
(1)根据上述数据完成下表:
(2)根据前面的统计分析,你认为平均数能较好地反映乙队游客的年龄特征吗?为什么?
甲队
| 年龄 | 13 | 14 | 15 | 16 | 17 |
| 人数 | 2 | 1 | 4 | 1 | 2 |
| 年龄 | 3 | 4 | 5 | 6 | 54 | 57 |
| 人数 | 1 | 2 | 2 | 3 | 1 | 1 |
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲队游客年龄 | 15 | 15 | 15 | 1.8 |
| 乙队游客年龄 | 15 | 5.5 | 6 | 11.4 |
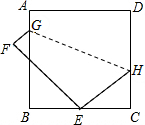 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,求线段EC,CH的长.
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,求线段EC,CH的长.