题目内容
19.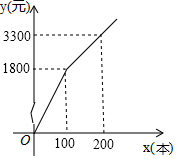 某书店为了迎接2017年4月23日的“世界读书日”,计划购进A、B两类图书进行销售,若购进A、B两类图书共1000本,其中购进A类图书的单价为16元/本,购进B类图书所需费用y(元)与购买数量x(本)之间存在如图所示的函数关系.
某书店为了迎接2017年4月23日的“世界读书日”,计划购进A、B两类图书进行销售,若购进A、B两类图书共1000本,其中购进A类图书的单价为16元/本,购进B类图书所需费用y(元)与购买数量x(本)之间存在如图所示的函数关系.(1)求y与x之间的函数关系式;
(2)若该书店购进A类图书400本,则购进A、B两类图书共需要多少元?
分析 (1)根据函数图象可以分段求出各段对应的函数解析式;
(2)根据题意可以分别求得两类图书的花费,从而可以求得两类图书总的花费.
解答 解:(1)当0≤x≤100时,设y与x之间的函数关系式是y=kx,
100k=1800,
解得,k=18,
即当0≤x≤100时,y与x之间的函数关系式是y=18x,
当x>100时,设y与x之间的函数关系式是y=ax+b,
$\left\{\begin{array}{l}{100a+b=1800}\\{200a+b=3300}\end{array}\right.$,解得,$\left\{\begin{array}{l}{a=15}\\{b=300}\end{array}\right.$,
即当x>100时,y与x之间的函数关系式是y=15x+300,
∴y与x之间的函数关系式是:y=$\left\{\begin{array}{l}{18x}&{(0≤x≤100)}\\{15x+300}&{(x>100)}\end{array}\right.$;
(2)书店购进A类图书400本,则购进B类图书600本,
则A类图书花费:400×16=6400(元),
B类图书花费:15×600+300=9300(元),
∴购进A、B两类图书共需要:6400+9300=15700(元),
答:购进A、B两类图书共需要15700元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用一次函数的性质解答.

练习册系列答案
相关题目
14. 如图,是某几何体的俯视图,则该几何体可能是( )
如图,是某几何体的俯视图,则该几何体可能是( )
 如图,是某几何体的俯视图,则该几何体可能是( )
如图,是某几何体的俯视图,则该几何体可能是( )| A. |  | B. |  | C. |  | D. |  |
8. 如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
 如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )
如图,将一块三角板的45°顶点放在直尺的一边上,当∠1=63°时,∠2=( )| A. | 108° | B. | 72° | C. | 77° | D. | 82° |
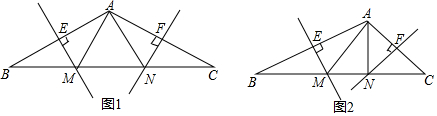
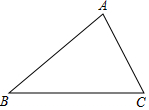 如图,已知△ABC,∠B=40°.
如图,已知△ABC,∠B=40°.
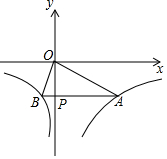 已知函数y=$\left\{\begin{array}{l}-\frac{12}{x}({x>0})\\ \frac{3}{x}({x<0})\end{array}$的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
已知函数y=$\left\{\begin{array}{l}-\frac{12}{x}({x>0})\\ \frac{3}{x}({x<0})\end{array}$的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论: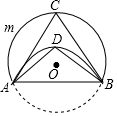 如图,将⊙O沿弦AB折叠,点C在$\widehat{AmB}$上,点D在$\widehat{AB}$上,若∠ACB=70°,则∠ADB=110°.
如图,将⊙O沿弦AB折叠,点C在$\widehat{AmB}$上,点D在$\widehat{AB}$上,若∠ACB=70°,则∠ADB=110°.