题目内容
19．
如图，下列A，B，C，D四个三角形中，能和模板中的△ABC完全重合的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 三条边分别对应相等的两个三角形全等；两边及其夹角分别对应相等的两个三角形全等；两角及其夹边分别对应相等的两个三角形全等；两角及其中一个角的对边对应相等的两个三角形全等，据此判断即可．
解答 解：A、∵a，c边夹角为50°，∴根据SAS可判定两三角形全等，故A正确；
B、∵a，c边夹角不一定为50°，∴不能判定两三角形全等，故B错误；
C、∵72°角所对的边不相等，∴不能判定两三角形全等，故C错误；
D、∵50°和58°的角的夹边不相等，∴不能判定两三角形全等，故D错误；
故选：A．
点评 本题主要考查了全等三角形的判定，解决问题的关键是掌握全等三角形的判定方法．全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件．
练习册系列答案
相关题目
9．
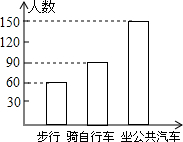如图，下列说法正确的是（ ）
如图，下列说法正确的是（ ）| A． | 步行人数最少，只为90人 | |
| B． | 步行人数为50人 | |
| C． | 步行与骑自行车的人数和比坐公共汽车的人数要多 | |
| D． | 坐公共汽车的人数占总数的50% |
10．
如图几何体从正面看是（ ）
如图几何体从正面看是（ ）| A． |  | B． |  | C． |  | D． |  |
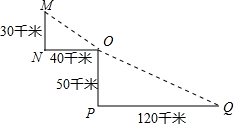如图是某沿江地区交通平面图，为了加快经济发展，该地区拟修建一条连接M，O，Q三城市的沿江高速的建设成本是100万元∕千米，该沿江高速的造价是多少？
杭州市推行垃圾分类已经多年，但在厨余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾，如图是杭州市某一天收到的厨余垃圾的统计图，则m的值为69.01．
11．对于分式$\frac{1}{a+1}$，总有（ ）
| A． | $\frac{1}{a-1}=\frac{2}{a-2}$ | B． | $\frac{1}{a-1}=\frac{a+1}{{{a^2}-1}}$（a≠-1） | ||
| C． | $\frac{1}{a-1}=\frac{a-1}{{{a^2}-1}}$ | D． | $\frac{1}{a-1}=\frac{-1}{a+1}$ |