题目内容
4.等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是斜边AB上一点,以CD为直角边作等腰Rt△CDE,其中∠DCE=90°,CD=CE,直线BC、DE交于点F.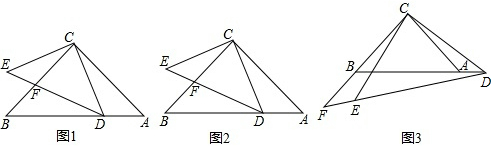
(1)如图1,若CD=DF,求证:AD=($\sqrt{2}$-1)BD;
(2)如图2,若BD=2AD,判断DF与EF之间的数量关系,并证明;
(3)如图3,当点D在BA的延长线上时,若AB=kAD,则DF=(k+1)EF.(用含k的式子表示)
分析 (1)先利用等腰直角三角形的性质和勾股定理可以求得AB=$\sqrt{2}$BC,然后再根据CD=DF可得出∠CFD=∠DCF,进而可得∠BDC=∠DCF,则有BC=BD,于是可得出结论;
(2)根据各角之间的关系可证得△CEF∽△CAD,△BCD∽△DCF,则有$\frac{DF}{BD}=\frac{CE}{CA},\frac{EF}{AD}=\frac{CD}{CB}$,再根据CE=CD,CA=CB,可得$\frac{DF}{BD}=\frac{EF}{AD}$,则可得出$\frac{EF}{DF}=\frac{1}{2}$;(3)首先证明△CAD∽△CEF,△BCA∽△ECA,根据相似三角形的对应边的比相等即可证得$\frac{AD}{EF}=\frac{AB}{CD}$,从而求解.
解答 解:(1)∵等腰Rt△ABC中,∠ACB=90°,AC=BC
∴根据勾股定理可得AB=$\sqrt{2}$BC,∠B=∠A=45°,
∵CD=DF,等腰Rt△CDE,
∴∠CFD=∠DCB,∠E=∠CDE=45°,
∵∠CFD=∠BDF+∠B=∠BDF+45°,∠CDB=∠BDF+∠CDE=∠BDF+45°,
∴∠CFD=∠CDB,
∴∠DCB=∠CDB,
∴BD=BC,
∴AD=AB-BD=$\sqrt{2}$BD-BD=($\sqrt{2}$-1)BD;
(2)DF=2EF.
证明:∵∠ACB=∠DCE=90°,
∴∠ACB-∠BCD=∠DCE-∠BCD,
∴∠ECB=∠ACD,
由(1)知∠B=∠A=∠E=∠CDE=45°,∠CFD=∠CDB,
∴△CEF∽△CAD,△BCD∽△DCF,
∴$\frac{DF}{BD}=\frac{CE}{CA},\frac{EF}{AD}=\frac{CD}{CB}$,
∵CE=CD,CA=CB,
∴$\frac{DF}{BD}=\frac{EF}{AD}$
∴$\frac{DF}{EF}=\frac{BD}{AD}=\frac{1}{2}$
(3)解:∵△BCA和△ECD都是等腰直角三角形,
∴得∠FCE=∠ACD,∠CEF=∠CAD=135°,
∴△CAD∽△CEF
∴$\frac{AD}{EF}=\frac{CA}{CE}$
又∵△BCA∽△ECA,
∴$\frac{BA}{ED}=\frac{CA}{CD}=\frac{CA}{CE}$
∴$\frac{AD}{EF}=\frac{AB}{ED}$
∴$\frac{AD}{AB}=\frac{EF}{DE}$
又∵AB=kAD,
∴DE=kEF,
∴DF=(k+1)EF.
点评 本题考查的是等腰直角三角形的性质和相似三角形的判定与性质,(3)中由相似三角形的对应边的比相等,再根据等量代换得到$\frac{AD}{EF}=\frac{AB}{ED}$是关键.

| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
 小明在拼图时发现,用8个一样大的长方形恰好可以拼成一个大的长方形,如图1所示;小红看见了,说:“我来试一试!”结果小红七拼八凑,拼成了一个如图2所示的正方形,但中间留下了一个洞,恰好是边长为2mm的小正方形.则每个小长方形的长是10mm,宽是6mm.
小明在拼图时发现,用8个一样大的长方形恰好可以拼成一个大的长方形,如图1所示;小红看见了,说:“我来试一试!”结果小红七拼八凑,拼成了一个如图2所示的正方形,但中间留下了一个洞,恰好是边长为2mm的小正方形.则每个小长方形的长是10mm,宽是6mm.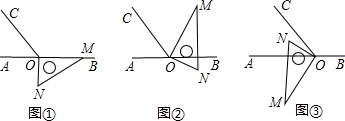
 将一副三角板拼成如图所示的图案,则∠ACD的度数为105°.
将一副三角板拼成如图所示的图案,则∠ACD的度数为105°.