题目内容
双曲线y=
(k>0),点A(m,n)(m>0)在此双曲线上,过点A作AB垂直y轴交y轴于点B.点C在线段AB上,过点C作直线CD⊥x轴于点D,交此双曲线于点P.
(1)请根据题意画出示意图;
(2)直线PA交y轴于点E,若AC=CP=2,且△OPE的面积是2n,求此双曲线的解析式.
| k |
| x |
(1)请根据题意画出示意图;
(2)直线PA交y轴于点E,若AC=CP=2,且△OPE的面积是2n,求此双曲线的解析式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据题意画出图形即可;
(2)求出P、C的坐标,求出直线AP的解析式,求出E的坐标,根据三角形面积得出关于n的方程,求出n的值,即可得出答案.
(2)求出P、C的坐标,求出直线AP的解析式,求出E的坐标,根据三角形面积得出关于n的方程,求出n的值,即可得出答案.
解答:解:(1)如图,
 ;
;
(2)∵A(m,n),
∴C(m-2,n),P(m-2,n+2),
∵A在双曲线上,
∴mn=k,
∵P在双曲线上,
∴(m-2)(n+2)=k,
∴mn+2m-2n-4=k,
∴m=n+2,
∴直线AP的解析式是y-n=-x+n+2,
当x=0时,y=2n+2,
∴E的坐标是(0,2n+2),
∵△OPE的面积是2n,
∴
(2n+2)(n+2-2)=2n,
解得:n=1,n=0(舍去),
∴m=3,
∴k=mn=3,
即此双曲线的解析式是y=
.
 ;
;(2)∵A(m,n),
∴C(m-2,n),P(m-2,n+2),
∵A在双曲线上,
∴mn=k,
∵P在双曲线上,
∴(m-2)(n+2)=k,
∴mn+2m-2n-4=k,
∴m=n+2,
∴直线AP的解析式是y-n=-x+n+2,
当x=0时,y=2n+2,
∴E的坐标是(0,2n+2),
∵△OPE的面积是2n,
∴
| 1 |
| 2 |
解得:n=1,n=0(舍去),
∴m=3,
∴k=mn=3,
即此双曲线的解析式是y=
| 3 |
| x |
点评:本题考查了用待定系数法求出反比例函数的解析式,三角形面积的应用,主要考查学生的计算能力,题目是一道比较典型的题目,难度适中.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
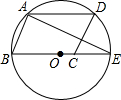 如图,平行四边形ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
如图,平行四边形ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )| A、27° | B、36° |
| C、46° | D、63° |
 1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度AB为37m,高为7m.
1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度AB为37m,高为7m.