题目内容
8.正六边形的周长为6mm,则它的面积为( )| A. | $\frac{\sqrt{3}}{2}$mm2 | B. | $\frac{3\sqrt{3}}{2}$mm2 | C. | 3$\sqrt{3}$mm2 | D. | 6$\sqrt{3}$mm2 |
分析 首先根据题意画出图形,即可得△OBC是等边三角形,又由正六边形ABCDEF的周长为6mm,即可求得BC的长,继而求得△OBC的面积,则可求得该六边形的面积.
解答 解:如图,连接OB,OC,过O作OM⊥BC于M,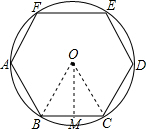
∴∠BOC=$\frac{1}{6}$×360°=60°,
∵OB=OC,
∴△OBC是等边三角形,
∵正六边形ABCDEF的周长为6mm,
∴BC=6÷6=1mm,
∴OB=BC=1mm,
∴BM=$\frac{1}{2}$BC=$\frac{1}{2}$mm,
∴OM=$\sqrt{{OB}^{2}{-BM}^{2}}$=$\frac{\sqrt{3}}{2}$mm,
∴S△OBC=$\frac{1}{2}$×BC×OM=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$mm2,
∴该六边形的面积为:$\frac{\sqrt{3}}{4}$×6=$\frac{3\sqrt{3}}{2}$mm2,
故选B.
点评 此题主要考查了圆的内接六边形的性质与等边三角形的判定与性质,注意掌握数形结合思想是解答此题的关键.

练习册系列答案
相关题目
13.某校举办初中生演讲比赛,每班派一名学生参赛,现某班有A、B、C三名学生竞选,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表和图1:
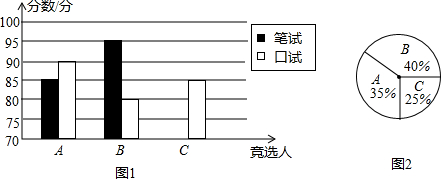
(1)请将表和图1中的空缺部分补充完整;
(2)竞选的最后一个程序是由本校的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按4:3:3的比例确定最后成绩,请计算学生A的最后成绩.
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |

(1)请将表和图1中的空缺部分补充完整;
(2)竞选的最后一个程序是由本校的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按4:3:3的比例确定最后成绩,请计算学生A的最后成绩.
20. 如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
 如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )
如图,是我县2013年11月份某天的天气预报,则这一天的最高气温比最低气温高( )| A. | -10℃ | B. | 10℃ | C. | 14℃ | D. | -14℃ |
17.已知△ABC∽△DEF,∠A=50°,∠B=30°,则∠F的值为( )
| A. | 50° | B. | 30° | C. | 80° | D. | 100° |
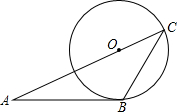 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=6,则$\widehat{BC}$的长为( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=6,则$\widehat{BC}$的长为( )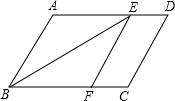 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过E作EF∥AB交BC于点F.
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过E作EF∥AB交BC于点F.