题目内容
5.如图,已知数轴上A、B两点表示的数分别为a、b,点P是数轴上任意一点(异于点A、B).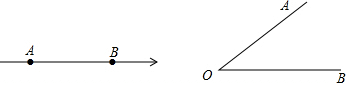
(1)线段AB的长度为b-a;
(2)若AP-AB=1,求点P表示的数;
(3)若点P在点B的右侧,点M、N分别是线段AP和线段BP的中点,则MN的长度为$\frac{b-a}{2}$;
(4)线段与角的很多知识都可用类比的思想学习研究,请你类比第(3)问设计一道以∠AOB为背景的问题,画出示意图并给出解答.
分析 (1)根据题意即可得到结果;
(2)①若点P在A的左侧,设点P表示的实数为x,②若点P在A的右侧,设点P表示的实数为x,列方程即可得到结论;
(3)如图,由点M、N分别是线段AP和线段BP的中点,得到PM=$\frac{1}{2}$AP=$\frac{1}{2}$(AB+PB),PN=$\frac{1}{2}$BP,根据线段的和差即可得到结论.
(4)由OM,ON分别平分∠AOP,∠BOP,得到∠POM=$\frac{1}{2}$∠AOP,∠PON=$\frac{1}{2}$∠BOP,根据角的和差即可得到结论.
解答 解:(1)线段AB的长度为b-a,
故答案为:b-a;
(2)①若点P在A的左侧,设点P表示的实数为x,
则a-x-(b-a)=1,
∴x=2a-b-1;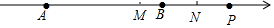
②若点P在A的右侧,设点P表示的实数为x,
则x-a-(b-a)=1,
∴x=b+1;
综上所述:点P表示的数为2a-b-1或b+1;
(3)如图,∵点M、N分别是线段AP和线段BP的中点,
∴PM=$\frac{1}{2}$AP=$\frac{1}{2}$(AB+PB),PN=$\frac{1}{2}$BP,
∴MN=PM-PN=$\frac{1}{2}$AB=$\frac{b-a}{2}$;
(4)题目:如图,∠AOB=m°,射线OP在∠AOB的外部,射线OM,ON分别平分∠AOP,∠BOP,求∠MON.
解:∵OM,ON分别平分∠AOP,∠BOP,
∴∠POM=$\frac{1}{2}$∠AOP,∠PON=$\frac{1}{2}$∠BOP,
∴∠POM-∠PON=$\frac{1}{2}∠$AOP-$\frac{1}{2}∠$BOP=$\frac{1}{2}$(∠AOP-∠BOP)=$\frac{1}{2}∠$AOB,
∵∠AOB=m°,
∴∠MON=∠POM-∠PON=$\frac{1}{2}$m°.
点评 本题考查了数轴和一元一次方程的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.

 如图,四边形ABCD是⊙O的内接四边形,若∠A=60°,则∠C的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠A=60°,则∠C的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
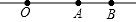 如图,下列不正确的说法是( )
如图,下列不正确的说法是( )| A. | 直线AB与直线BA是同一条直线 | B. | 射线OA与射线AB是同一条射线 | ||
| C. | 线段AB与线段BA是同一条线段 | D. | 射线OA与射线OB是同一条射线 |
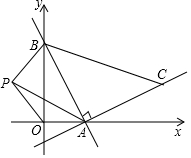 如图,一次函数y=-2x+4与x轴,y轴分别交于A,B,以线段AB为直角边在第一象限内作Rr△ABC,使AB=AC.
如图,一次函数y=-2x+4与x轴,y轴分别交于A,B,以线段AB为直角边在第一象限内作Rr△ABC,使AB=AC.