题目内容
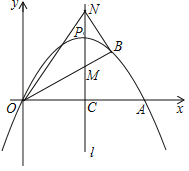
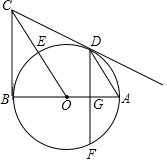
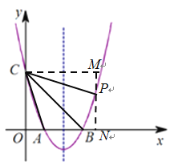
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求该抛物线的表达式及顶点坐标;
(2)点![]() 为抛物线上一点(不与点
为抛物线上一点(不与点![]() 重合),联结
重合),联结![]() .当
.当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,将抛物线沿平行于![]() 轴的方向向下平移,平移后的抛物线的顶点为点
轴的方向向下平移,平移后的抛物线的顶点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,当
,当![]() 时,求抛物线平移的距离.
时,求抛物线平移的距离.
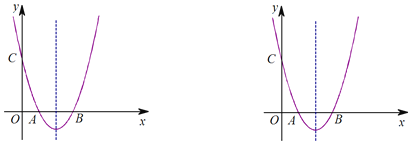
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)抛物线平移的距离为
;(3)抛物线平移的距离为![]() .
.
【解析】
(1)根据点A的坐标及对称轴可以先得出点B的坐标,再将A,B的坐标代入表达式即可求出结果,进而得出顶点坐标;
(2)由∠PCB=∠ACB和∠ABC=45°联想到构造全等三角形,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,可得出
,可得出![]() ,再由
,再由![]() ,可得出
,可得出![]() .设PM=a,用a表示出点P的横坐标,代入解析式,可求出a的值,进而得出点P的坐标.
.设PM=a,用a表示出点P的横坐标,代入解析式,可求出a的值,进而得出点P的坐标.
(3)过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,可得
,可得![]() ,根据
,根据![]() ,得
,得![]() ,用含m的式子表示出OE,QF的长,然后列出关于m的方程,求出m即可.
,用含m的式子表示出OE,QF的长,然后列出关于m的方程,求出m即可.
解:(1)∵![]() 的坐标为
的坐标为![]() ,对称轴为直线
,对称轴为直线![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]()
将![]() 、
、![]() 代入
代入![]() ,得
,得
![]() 解得:
解得:![]()
所以,![]() .
.
当![]() 时,
时,![]() ,
,
∴顶点坐标为![]() .
.
(2)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
∵![]() ,∴四边形
,∴四边形![]() 为矩形.
为矩形.
∴![]() ,
,![]() .
.
∵![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() .∴
.∴![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
∴![]() .
.
将![]() 代入
代入![]() ,得
,得
![]() .
.
解得![]() ,
,![]() (舍).∴
(舍).∴![]() .
.
(3)设抛物线平移的距离为![]() ,如图.得
,如图.得![]() ,
,
∴![]() 的坐标为
的坐标为![]() .
.
过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.

∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴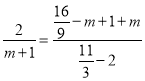 .
.
解得![]() .
.
即抛物线平移的距离为![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目