题目内容
若一组数据1,1,2,3,4,x的平均数是2,则这组数据的中位数是 ,方差是 .
考点:方差,算术平均数,中位数
专题:
分析:先根据平均数的计算公式先求出x的值,再根据中位数和方差公式分别进行解答即可.
解答:解:∵数据1,1,2,3,4,x的平均数是2,
∴(1+1+2+3+4+x)÷6=2,
解得:x=1,
把这组数据从小到大排列为:1,1,1,2,3,4,
最中间两个数的平均数是(1+2)÷2=1.5,
则这组数据的中位数是1.5;
方差是
[3×(1-2)2+(2-2)2+(3-2)2+(4-2)2]=
;
故答案为:1.5,
.
∴(1+1+2+3+4+x)÷6=2,
解得:x=1,
把这组数据从小到大排列为:1,1,1,2,3,4,
最中间两个数的平均数是(1+2)÷2=1.5,
则这组数据的中位数是1.5;
方差是
| 1 |
| 6 |
| 4 |
| 3 |
故答案为:1.5,
| 4 |
| 3 |
点评:此题考查了中位数和方差,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数;一般地设n个数据x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2].
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
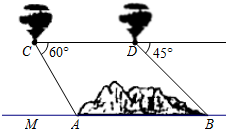 如图,我省在修建泛亚铁路时遇到一座山,要从A地向B地修一条隧道(A,B在同一水平面上),为了测量A,B两地之间的距离,某工程师乘坐热气球从M地出发垂直上升150 米到达C处,在C处观察A地的俯角为60°,然后保持同一高度向前平移200米到达D处,在D处观察B地的俯角为45°,则A、B两地之间的距离为多少米?(参考数据:
如图,我省在修建泛亚铁路时遇到一座山,要从A地向B地修一条隧道(A,B在同一水平面上),为了测量A,B两地之间的距离,某工程师乘坐热气球从M地出发垂直上升150 米到达C处,在C处观察A地的俯角为60°,然后保持同一高度向前平移200米到达D处,在D处观察B地的俯角为45°,则A、B两地之间的距离为多少米?(参考数据: 如图所示,一个半径为1的圆过一个半径为
如图所示,一个半径为1的圆过一个半径为