题目内容
若平面内有一正方形ABCD,M是该平面内任意点,则
的最小值为 .
| MA+MC |
| MB+MD |
考点:正弦定理与余弦定理
专题:计算题
分析:过点M作MF⊥AD交AD的延长线与点F,作ME垂直BC交BC的延长线与点E,则可得出MA2+MC2=MB2+MD2,利用余弦定理表示出AC2、BD2,根据AC=BD可得出
的值,进而表示出
,转化为求
的最小值,然后可判断出点M的位置.
| MA•MC |
| MB•MD |
| MA+MC |
| MB+MD |
| MA•MC |
| MB•MD |
解答:解:过点M作MF⊥AD交AD的延长线与点F,作ME垂直BC交BC的延长线与点E,如图,
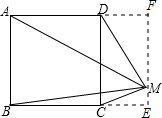
∵MA2+MC2=MF2+AF2+ME2+CE2,MB2+MD2=BE2+ME2+DF2+FM2,DF=CE,AF=BE,
∴MA2+MC2=MB2+MD2,
又∵AC2=MA2+MC2-2MA•MC•cos∠AMC,BD2=MB2+MD2-2MB•MD•cos∠BMD,AC=BD,
∴MA•MC•cos∠AMC=MB•MD•cos∠BMD,
=
,
∵
=
,
又∵MA2+MC2=MB2+MD2,
∴当
最小时,这个值最小,所以当∠BMD=90°,∠AMC=0°时最小,即点M与点A、C重合时,
此时
=
.
故答案为:
.

∵MA2+MC2=MF2+AF2+ME2+CE2,MB2+MD2=BE2+ME2+DF2+FM2,DF=CE,AF=BE,
∴MA2+MC2=MB2+MD2,
又∵AC2=MA2+MC2-2MA•MC•cos∠AMC,BD2=MB2+MD2-2MB•MD•cos∠BMD,AC=BD,
∴MA•MC•cos∠AMC=MB•MD•cos∠BMD,
| MA•MC |
| MB•MD |
| cos∠BMD |
| cos∠AMC |
∵
| MA+MC |
| MB+MD |
|
又∵MA2+MC2=MB2+MD2,
∴当
| cos∠BMD |
| cos∠AMC |
此时
| MA+MC |
| MB+MD |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:此题考查了余弦定理的知识,难度较大,解答本题的关键是将原式的最小值转化为求
最小值,另外要求我们熟练掌握勾股定理的应用.
| cos∠BMD |
| cos∠AMC |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
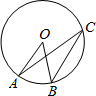 如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=40°,则∠OAC的度数等于( )
如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=40°,则∠OAC的度数等于( )| A、40° | B、60° |
| C、50° | D、20° |
若a4+3a2=1,b2-3b=1,且a2b≠1,则
的值是( )
| a2b+1 |
| a2 |
| A、3 | B、2 | C、-3 | D、-2 |
 如图,△ABC中,∠C=90°,∠ABC和∠EAC的平分线交于点D,∠ABD和∠BAD的平分线交于点F,则∠AFB的度数为
如图,△ABC中,∠C=90°,∠ABC和∠EAC的平分线交于点D,∠ABD和∠BAD的平分线交于点F,则∠AFB的度数为
 如图,草坪上的自动喷水装置能旋转220°,若它的喷射半径是20m,则它能喷灌的草坪的面积为
如图,草坪上的自动喷水装置能旋转220°,若它的喷射半径是20m,则它能喷灌的草坪的面积为