题目内容
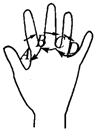
如图,在各个手指间标记字母A,B,C,D.请按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,….当字母C第2015次出现时,数到的数恰好是__________.
6045.
【考点】规律型:数字的变化类.
【分析】由图中可以看出:A→B→C→D→C→B→A→B→C→…,6个字母一循环,在这一个循环里面,C出现2次,利用2015次除以2得出循环的次数与余数判定数的个数,由此规律解决问题.
【解答】解:∵字母A→B→C→D→C→B每6个一循环,在这一个循环里面,C出现2次,2015÷2=1007…1,
∴C第2015次出现时,数到的数恰好是1007×6+3=6045.
故答案为:6045.
【点评】此题考查图形的变化规律,找出数字的运算规律,得出运算的方法解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B. C.
C.
 D.
D.
 (1×2×3﹣0×1×2)
(1×2×3﹣0×1×2)