题目内容
如图,△ABC为等边三角形,AD为BC边上的高,E为AC边上的一点,且AE=AD,则∠EDC=__________.
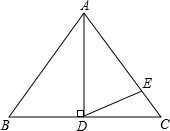
15°.
【考点】等边三角形的性质.
【分析】先根据等边三角形的性质得出∠BAC=60°,再由AD⊥BC得出∠CAD的度数,根据AE=AD求出∠ADE的度数,由∠EDC=∠ADC﹣∠ADE即可得出结论.
【解答】解:∵△ABC是等边三角形,
∴∠BAC=60°.
∵AD⊥BC,
∴∠CAD=30°,∠ADC=90°,
∵AE=AD,
∴∠ADE= =75°,
=75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
故答案为:15°.
【点评】本题考查的是等边三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B.
B. 
 0,则ab=__________.
0,则ab=__________.
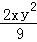 的系数为﹣2;
的系数为﹣2; 
 的系数是( )
的系数是( ) B.﹣
B.﹣ D.﹣
D.﹣