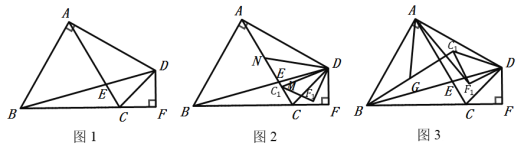
题目内容
【题目】在矩形![]() 中,
中,![]() 为
为![]() 的平分线.
的平分线.

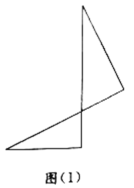
(1)如图①,若矩形![]() 是正方形,
是正方形,![]() ,求
,求![]() 的长;
的长;
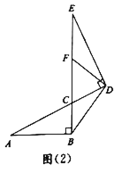
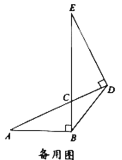
(2)如图②,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图②,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用角平分线的性质证得![]() ,由Rt△ABE
,由Rt△ABE![]() Rt△FBE,推出AB=BF,再求得对角线的BD长,设
Rt△FBE,推出AB=BF,再求得对角线的BD长,设![]() ,在
,在![]() 中,利用勾股定理构建方程即可求解;
中,利用勾股定理构建方程即可求解;
(2)同理证得![]() ,AB=BF,求得对角线的BD长,设
,AB=BF,求得对角线的BD长,设![]() ,在
,在![]() 中,利用勾股定理构建方程即可求解;
中,利用勾股定理构建方程即可求解;
(3)同理,设![]() ,在
,在![]() 中,利用勾股定理构建方程即可求解.
中,利用勾股定理构建方程即可求解.
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
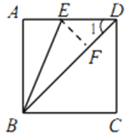
∵![]() ,即
,即![]() ,
,![]() 为
为![]() 的平分线,
的平分线,
∴![]() ,
,
∵BE公共,
∴Rt△ABE![]() Rt△FBE,
Rt△FBE,
∴AB=BF=1,
∵四边形![]() 是正方形,
是正方形,
∴AB=AD=1,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴EF=FD,
设![]() ,则
,则![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
即![]() ,
,
解得:![]() (负值已舍),
(负值已舍),
即![]() ;
;
(2)如图,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
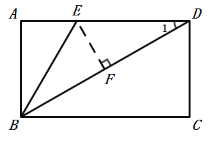
同理可得:![]() ,AB=BF=1,
,AB=BF=1,
![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
即![]() ,
,
解得:![]() ,
,
即![]() ;
;
(3)如图,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.

同理可得:![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
即![]() ,
,
解得:![]() ,
,
即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目