题目内容
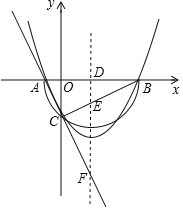
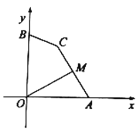
【题目】如图，点A，B的坐标分别为
，点C为坐标平面内一点，
，点M为线段
的中点，连接
，则的最大值为（ ）
A.
B.
C.
D.
【答案】B
【解析】
如图所示，取AB的中点N，连接ON，MN，根据三角形的三边关系可知OM＜ON+MN，则当ON与MN共线时，OM= ON+MN最大，再根据等腰直角三角形的性质以及三角形的中位线即可解答．
解：如图所示，取AB的中点N，连接ON，MN，三角形的三边关系可知OM＜ON+MN，则当ON与MN共线时，OM= ON+MN最大，
∵
，
则△ABO为等腰直角三角形，
∴AB=
，N为AB的中点，
∴ON=
，
又∵M为AC的中点，
∴MN为△ABC的中位线，BC=1，
则MN=
，
∴OM=ON+MN=
，
∴OM的最大值为
故答案选：B．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
