Question

8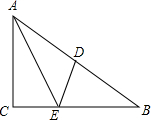．如图，在Rt△ABC中，∠ACB=90°，点D为AB中点，点E在BC边上，BE=AD，AE=6，∠AED=45°，则线段AC的长为$\frac{12\sqrt{5}}{5}$．

Answer 1

分析 如图，作AG⊥ED于G，BH⊥ED于H．首先证明AG=EG=3$\sqrt{2}$，由△ADG≌△BDH，推出DH=DG=EH=$\sqrt{2}$，设AC=x，EC=y，利用勾股定理构建方程组即可解决问题．

解答 解：如图，作AG⊥ED于G，BH⊥ED于H．

∵AD=BD=BE，BH⊥DE，
∴HD=HE，
∵∠AGE=90°，∠AEG=45°，
∴∠GAE=∠GEA=45°，
∵AE=6，
∴GA=GE=3$\sqrt{2}$，
在△ADG和△BDH中，
$\left\{\begin{array}{l}{∠ADG=∠BDH}\\{∠G=∠BHD}\\{AD=BD}\end{array}\right.$，
∴△ADG≌△BDH，
∴DH=DG=EH=$\sqrt{2}$，
在Rt△ADG中，AD=$\sqrt{A{G}^{2}+D{G}^{2}}$=2$\sqrt{5}$，
∴AB=4$\sqrt{5}$，设AC=x，EC=y，
则有$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=36}\\{{x}^{2}+（x+2\sqrt{5}）^{2}=80}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=\frac{12\sqrt{5}}{5}}\\{y=\frac{6\sqrt{5}}{5}}\end{array}\right.$．
∴AC=$\frac{12\sqrt{5}}{5}$．
故答案为$\frac{12\sqrt{5}}{5}$．

点评 本题考查全等三角形的判定和性质、二元二次方程组、勾股定理等知识，解题的关键是学会添加常用辅助线，构造特殊三角形解决问题，属于中考常考题型．