题目内容
三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
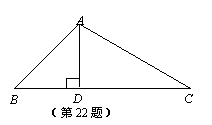
已知△ABC中,AB= ,∠B=45°,BC=1+
,∠B=45°,BC=1+ ,解△ABC.
,解△ABC.
 |
解:过点A作AD⊥BC,垂足为D.
在Rt△ADB中,∠ADB=90°,∠B=45°,AB=
则cos∠B=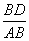 .
.
∴AD=BD= AB×cos 45°=
AB×cos 45°= ×cos 45°=1.
×cos 45°=1.
在Rt△ADC中,∠ADC=90°,C D=BC-BD=1+
D=BC-BD=1+ -1=
-1= .
.
则tan∠C=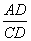 =
=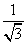 =
= .
.
∴∠C=30°.
∴AC=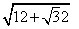 =2,∠BAC=180°-45°-30°=105°.
=2,∠BAC=180°-45°-30°=105°.
 |

为了解南京市民每天的阅读时间情况,随机抽取了部分市民进行调查,根据调查结果绘制如下尚不完整的频数分布表:
| 阅读时间 x(min) | 0≤x<30 | 30≤x<60 | 60≤x<90 | x≥90 | 合计 |
| 频数 | 450 | 400 | ② | 50 | ④ |
| 频率 | ① | 0.4 | 0.1 | ③ | 1 |
(1)补全表格中①~④的数据;
(2)将每天阅读时间不低于60 min的市民称为“阅读爱好者”,若我市约有800万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?
△ABC中,AB=AC=10,BC=12,矩形DEFG中,EF=4,FG>12.
(1)如图①,点A是FG的中点,FG∥BC,将矩形DEFG向下平移,直到DE与BC重合为止.要研究矩形DEFG与△ABC重叠部分的面积,就要进行分类讨论,你认为如何进行分类,写出你的分类方法(无需求重叠部分的面积).
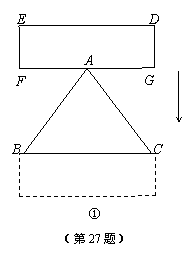 |
(2)如图②,点B与F重合,E、B、C在同一直线上,将矩形DEFG向右平移,直到点E与C重合为止.设矩形DEFG与△ABC重叠部分的面积为y,平移的距离为x.
① 求y与x的函数关系式,并写出自变量的取值范围;
② 在给定的平面直角坐标系中画出y与x的大致图象,并在图象上标注出关键点坐标.
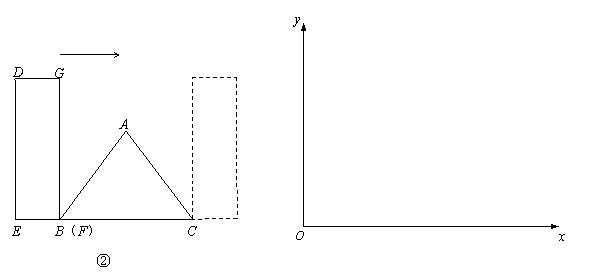 |
 有意义的x的取值范围是
有意义的x的取值范围是  ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来. 的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线长为( )
的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线长为( ) C.1 D.
C.1 D.

