��Ŀ����
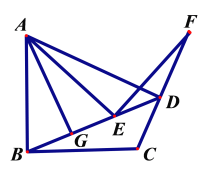
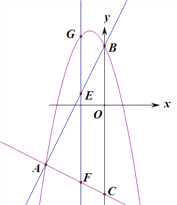
����Ŀ����ͼ��������y=-x2+bx+c��ֱ��AB����A(-4��-4)��B(0��4)���㣬ֱ��AC��y=-![]() x-6��y�����C.��E��ֱ��AB�ϵĶ��㣬����E��EF��x�ύAC�ڵ�F�����������ڵ�G.
x-6��y�����C.��E��ֱ��AB�ϵĶ��㣬����E��EF��x�ύAC�ڵ�F�����������ڵ�G.
��1����������y=-x2+bx+c�ı���ʽ��
��2������GB��EO�����ı���GEOB��ƽ���ı���ʱ�����G�����ꣻ
��3������y���ϴ���һ��H������EH��HF������E�˶���ʲôλ��ʱ����A��E��F��HΪ������ı����Ǿ��Σ������ʱ��E��H�����ꣻ
���ڢٵ�ǰ���£��Ե�EΪԲ�ģ�EH��Ϊ�뾶��Բ����MΪ��E��һ���㣬��![]() AM+CM����Сֵ.
AM+CM����Сֵ.
���𰸡���1��y=-x2-2x+4����2��G(-2��4)����3����H(0��-1)����![]()
����������������1�����ô���ϵ������������߽���ʽ��
��2�������ô���ϵ�������ֱ��AB�Ľ���ʽ����������ƽ���ı��εĶԱ���Ƚ���������⼴�ɣ�
��3�������жϳ�Ҫ�Ե�A��E��F��HΪ������ı����Ǿ��Σ�ֻ��EFΪ�Խ��ߣ������е����깫ʽ�������̼��ɣ�
����ȡEG���е�P�����жϳ���PEM�ס�MEA���ɵó�PM=![]() AM������CP��ԲE��M���������P�����꼴�ɵó����ۣ�
AM������CP��ԲE��M���������P�����꼴�ɵó����ۣ�
��⣺��1����1���ߵ�A��-4��-4����B��0��4����������y=-x2+bx+c�ϣ�
��![]() ��
��
��![]() ��
��
�������ߵĽ���ʽΪy=-x2-2x+4��
��2����ֱ��AB�ı���ʽΪy=kx+b
��ֱ��AB����A(-4��-4)��B(0��4)��
��![]() �����
�����![]() ��
��
��y=2x+4
��E(m��2m+4)����G(m��-m2-2m+4)
���ı���GEOB��ƽ���ı��Σ�
��GE=OB=4��
��-m2-2m+4-2m-4=4�����m=-2
��G(-2��4)
��3������E(m��2m+4)����F(m��-![]() m-6)
m-6)
��A��AN��EG����H��HQ��EG
�ı���AFHE�Ǿ��Σ����PFN�ա�HEQ����AN=QH����m+4=-m�����m=-2��E(-2��0)
EQ=FN=-4+![]() m+6=1
m+6=1
��H(0��-1)


��������ɵã�E(-2��0)��H(0��-1),��EH=![]() ������E�İ뾶Ϊ
������E�İ뾶Ϊ![]() ��
��
��M���ڡ�E�ϣ���EM=![]()
��A(-4��-4)��E(-2��0)����AE=2![]()
��AE�Ͻ�ȡEP=![]() EM����EP=
EM����EP=![]() ������PM��
������PM��
����EPM����EMA����![]() =
=![]() =
=![]() =
=![]() =
=![]() ����PEM=��MEA������EPM����EMA��PM=
����PEM=��MEA������EPM����EMA��PM=![]() AM
AM
���߶�PC�ij���Ϊ![]() AM+CM����Сֵ
AM+CM����Сֵ
��EP=![]() EM=
EM=![]() AE=
AE=![]() ��2
��2![]() =
=![]() ��AP=AE-PE=
��AP=AE-PE=![]() , AC=2
, AC=2![]() ��PC=
��PC=![]()
��![]() AM+CM����СֵΪ
AM+CM����СֵΪ![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�