题目内容
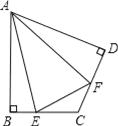
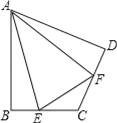
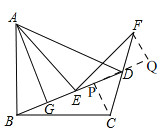
【题目】如图,在四边形ABCD中,AB=BC, ∠ABC=90 ,点E在BD上,点F在射线CD上,AE=EF,∠AEF=90 .
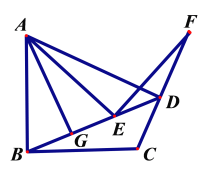
(1)若∠ABE=∠AEB,AG⊥BD,垂足为G,求证:BG=GE.
(2)在(1)的条件下,猜想线段CD与DF的数量关系,并证明你的猜想.
【答案】(1)详见解析;(2)CD=DF,理由详见解析.
【解析】
(1)由∠ABE=∠AEB可得AB=AE,根据等腰三角形三线合一的性质即可证得BG=GE;(2)CD=DF,过点C作CP⊥BD于P,过点F作FQ⊥BD交BD的延长线于Q,证明△BCP≌△EFQ,根据全等三角形的性质可得CP=FQ,再证明△CPD≌△FQD,根据全等三角形的对应边相等即可证得结论.
(1)∵∠ABE=∠AEB,
∴AB=AE,
∵AG⊥BD,
∴BG=GE;
(2)CD=DF,理由如下:
如图,过点C作CP⊥BD于P,过点F作FQ⊥BD交BD的延长线于Q,
∴∠BPC=∠DPC=∠FQE=90°,
∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
∵∠ABE=∠AEB,
∴∠AEB+∠CBD=90°,
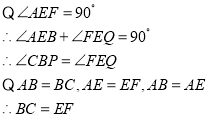
在△BCP和△EFQ中,
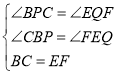
![]()
在△CPD和△FQD中,
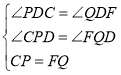
![]()

练习册系列答案
相关题目