题目内容
设A=2x2-3xy+y2-x+2y,B=4x2-6xy+2y2-3x-y,若|x-2a|+(y+3)2=0,且-2A+B=a,求A的值.
考点:整式的加减—化简求值,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:先代入求出-2A+B的值,根据绝对值和偶次方的非负性求出a=
x,y=-3,代入-2A+B=a求出x的值,即可求出答案.
| 1 |
| 2 |
解答:解:-2A+B=-2(2x2-3xy+y2-x+2y)+(4x2-6xy+2y2-3x-y)
=-4x2+6xy-2y2+2x-4y+4x2-6xy+2y2-3x-y
=-x-5y,
∵|x-2a|+(y+3)2=0,
∴x-2a=0,y+3=0,
∴a=
x,y=-3,
∵-2A+B=a,
∴-x-5(-3)=
x,
∴x=10,
∴A=2×102-3×10×(-3)+(-3)2-10+2×(-3)=283.
=-4x2+6xy-2y2+2x-4y+4x2-6xy+2y2-3x-y
=-x-5y,
∵|x-2a|+(y+3)2=0,
∴x-2a=0,y+3=0,
∴a=
| 1 |
| 2 |
∵-2A+B=a,
∴-x-5(-3)=
| 1 |
| 2 |
∴x=10,
∴A=2×102-3×10×(-3)+(-3)2-10+2×(-3)=283.
点评:本题考查了绝对值,偶次方,整式的混合运算的应用,解此题的关键是求出x、y的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
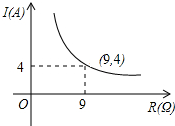 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示. 如图,在等腰三角形ABC中,AB=AC,D是BC的中点,过A作AE⊥DE,AF⊥DF,且AE=AF,求证:∠EDB=FDC.
如图,在等腰三角形ABC中,AB=AC,D是BC的中点,过A作AE⊥DE,AF⊥DF,且AE=AF,求证:∠EDB=FDC.