题目内容
11.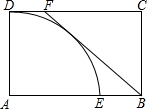 如图,矩形ABCD,AB=3,AD=2,以点A为圆心,AD长为半径的DE交AB于E,DF=0.8,判断直线BF与DE所在的圆的位置关系.
如图,矩形ABCD,AB=3,AD=2,以点A为圆心,AD长为半径的DE交AB于E,DF=0.8,判断直线BF与DE所在的圆的位置关系.
分析 若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答 解:连接AF,作AG⊥BF,FH⊥AB,如图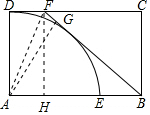 ,
,
FH=AD=2,D=AH=0.8,HB=2.2
由勾股定理,得FB=$\sqrt{F{H}^{2}+H{B}^{2}}$=$\sqrt{8.84}$<3.
S梯形ABDF=S△ABF+S△ADF,
$\frac{1}{2}$×2×0.8+$\frac{1}{2}$AG•FB=$\frac{1}{2}$(DF+AB)•AD,
化简得
AG•BF=6,
∵BF=$\sqrt{8.84}$<3,
∴AG>2,
即d>r,
直线BF与DE所在的圆的位置关系相离.
点评 本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.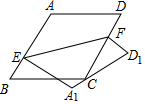 如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )
如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )
 如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )
如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}-1}{6}$ | C. | $\frac{\sqrt{3}+1}{8}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
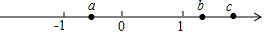 已知实数a,b,c在数轴上的位置如图所示.化简:$\sqrt{{a}^{2}}$+|a+c|-$\sqrt{(a-b)^{2}}$+|1-b|
已知实数a,b,c在数轴上的位置如图所示.化简:$\sqrt{{a}^{2}}$+|a+c|-$\sqrt{(a-b)^{2}}$+|1-b|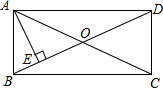 如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.
如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$. 七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.
七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1. 如图,AB是⊙O的直径,AB=4$\sqrt{3}$,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
如图,AB是⊙O的直径,AB=4$\sqrt{3}$,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.