题目内容
若一次函数y=-x+m2与y=4x-1的图象交于x轴,则m的值为 .
考点:两条直线相交或平行问题
专题:
分析:首先计算出y=4x-1与x轴交点为(
,0),再把(
,0)代入y=-x+m2可算出m的值.
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:y=4x-1中,当y=0时,x=
,
故y=4x-1的图象与x轴交点为(
,0),
∵一次函数y=-x+m2与y=4x-1的图象交于x轴,
∴一次函数y=-x+m2的图象过(
,0),
∴0=-
+m2,
解得:m=±0.5,
故答案为:±0.5.
| 1 |
| 4 |
故y=4x-1的图象与x轴交点为(
| 1 |
| 4 |
∵一次函数y=-x+m2与y=4x-1的图象交于x轴,
∴一次函数y=-x+m2的图象过(
| 1 |
| 4 |
∴0=-
| 1 |
| 4 |
解得:m=±0.5,
故答案为:±0.5.
点评:此题主要考查了两条直线相交,关键是掌握凡是函数图象经过的点必能满足解析式.

练习册系列答案
相关题目
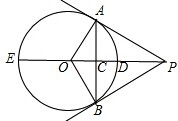 如图,PA、PB是⊙O的两条切线,点A、B为切点,直线OP交⊙O于点D、E,交AB于点C.
如图,PA、PB是⊙O的两条切线,点A、B为切点,直线OP交⊙O于点D、E,交AB于点C. 如图,△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC于点E,且BC=10cm,则△DCE的周长为
如图,△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC于点E,且BC=10cm,则△DCE的周长为 如图△ABC中,AB=AC,∠A=36°,CD是角平分线,则△DBC的周长与△ABC的周长的比值是
如图△ABC中,AB=AC,∠A=36°,CD是角平分线,则△DBC的周长与△ABC的周长的比值是 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题: