题目内容
 如图,PC为⊙O的切线,PM平分∠CPA,交CA、CB于E、F
如图,PC为⊙O的切线,PM平分∠CPA,交CA、CB于E、F (1)求证:∠PCE=∠B;
(2)若CE、CF为方程x2+(m-2)+m+1=0的两根,求CE的长.
考点:切线的性质,根与系数的关系
专题:
分析:(1)作直径CN,连接AN,根据圆周角定理求出∠B=∠N,∠NAC=90°,根据切线性质得出∠PCN=90°,即可得出答案;
(2)求出CF=CE,根据根的判别式求出m的值,得出一元二次方程,求出方程的解即可.
(2)求出CF=CE,根据根的判别式求出m的值,得出一元二次方程,求出方程的解即可.
解答:(1)证明: 作直径CN,连接AN,
作直径CN,连接AN,
则∠B=∠N,∠NAC=90°,
∵PC切⊙O于C,
∴∠PCN=90°,
∴∠PCA+∠ACN=90°,∠N+∠ACN=90°,
∴∠PCA=∠N=∠B;
(2)解:∵PM平分∠CPB,
∴∠CPM=∠BPM,
∵∠CPM+∠PCA=∠CEF,∠BPM+∠B=∠CFE,
∴∠CFE=∠CEF,
∴CF=CE,
∵CE、CF为方程x2+(m-2)+m+1=0的两根,
∴△=(m-2)2-4(m+1)=0,
解得:m=0或8,
即方程为①x2-2x+1=0,x2+6x+9=0,
解方程①得:x1=x2=1;
解方程②得:x3=x4═-3(舍去);
即CE=1.
 作直径CN,连接AN,
作直径CN,连接AN,则∠B=∠N,∠NAC=90°,
∵PC切⊙O于C,
∴∠PCN=90°,
∴∠PCA+∠ACN=90°,∠N+∠ACN=90°,
∴∠PCA=∠N=∠B;
(2)解:∵PM平分∠CPB,
∴∠CPM=∠BPM,
∵∠CPM+∠PCA=∠CEF,∠BPM+∠B=∠CFE,
∴∠CFE=∠CEF,
∴CF=CE,
∵CE、CF为方程x2+(m-2)+m+1=0的两根,
∴△=(m-2)2-4(m+1)=0,
解得:m=0或8,
即方程为①x2-2x+1=0,x2+6x+9=0,
解方程①得:x1=x2=1;
解方程②得:x3=x4═-3(舍去);
即CE=1.
点评:本题考查了切线的性质,圆周角定理,一元二次方程的根的判别式,解一元二次方程,三角形外角性质的应用,能综合运用知识点进行推理和计算是解此题的关键.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(-1)0=-1 | ||
| B、(-1)-1=1 | ||
C、3a-2=
| ||
| D、(-x)5÷(-x)-3=x2 |
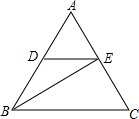 如图,在△ABC中,D是AB上一点,AB=3AD,DE∥BC,交AC于点E,若△ABC的面积为6,求△BED的面积.
如图,在△ABC中,D是AB上一点,AB=3AD,DE∥BC,交AC于点E,若△ABC的面积为6,求△BED的面积.