题目内容
19．
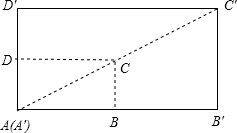如图，矩形ABCD与矩形A′B′C′D′是位似图形，A是位似中心，已知矩形ABCD的周长为24，BB′=4，DD′=2．求AB和AD的长．
分析 首先设AB=x，然后利用x表示出AD，AD′，AB′的长，再由矩形ABCD与矩形A′B′C′D′是位似图形，可得方程$\frac{12-x}{14-x}=\frac{x}{x+4}$，解此方程即可求得答案．
解答 解：设AB=x，
∵矩形ABCD的周长为24，
∴AD=12-x，
∵BB′=4，DD′=2，
∴AD′=AD+DD′=14-x，AB′=AB+BB′=x+4，
∵矩形ABCD与矩形A′B′C′D′是位似图形，
∴$\frac{AD}{AD′}=\frac{AB}{AB′}$，
即$\frac{12-x}{14-x}=\frac{x}{x+4}$，
解得：x=8，
经检验，x=8是原分式方程的解．
∴AB=8，AD=4．
点评 此题考查了位似图形的性质．注意根据题意构造方程是解此题关键．
练习册系列答案
相关题目
9．已知xy≠1，且有3x2+2014x+7=0，7y2+2014y+3=0，则$\frac{x}{y}$的值等于（ ）
| A． | $\frac{3}{7}$ | B． | $\frac{7}{3}$ | C． | -$\frac{2014}{7}$ | D． | -$\frac{2014}{3}$ |
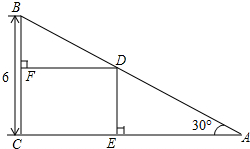王师傅想在一块三角形剩料中挖去一块最大矩形料做其他用途，其图形和数据如图所示，请你计算王师傅所取得最大矩形料的面积是9$\sqrt{3}$，这时CE=3，CF=3$\sqrt{3}$．
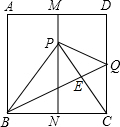如图，有一块面积为1的正方形ABCD，M、N分别为AD、BC边的中点，将C点折至MN上，落在点P的位置，折痕为BQ，连结PC交BQ于E．连结PQ．BP．
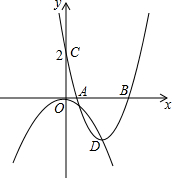如图，已知抛物线C1：y=-$\frac{1}{2}$x2，平移抛物线y=x2，使其顶点D落在抛物线C1位于y轴右侧的图象上，设平移后的抛物线为C2，且C2与y轴交于点C（0，2）．