题目内容
8.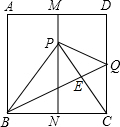 如图,有一块面积为1的正方形ABCD,M、N分别为AD、BC边的中点,将C点折至MN上,落在点P的位置,折痕为BQ,连结PC交BQ于E.连结PQ.BP.
如图,有一块面积为1的正方形ABCD,M、N分别为AD、BC边的中点,将C点折至MN上,落在点P的位置,折痕为BQ,连结PC交BQ于E.连结PQ.BP.(1)求证PB=PC;
(2)求MP的长度;
(3)求证:以PQ为边长的正方形的面积等于$\frac{1}{3}$.
分析 (1)根据折叠的性质,可得BQ垂直平分PC,进而可得△PBC是等边三角形;
(2)由(1)中的等边三角形可得PN的值.根据图形的关系可MP=MN-PN,代入数据可得答案;
(3)根据折叠的性质,可得PQ=QC,∠PBQ=∠QBC=30°;再在Rt△BCQ中,根据三角函数的定义可求得PQ的值,进而可得答案.
解答  (1)解:由折法知点P是点C关于折痕BQ的对称点.
(1)解:由折法知点P是点C关于折痕BQ的对称点.
∴BQ垂直平分PC,BC=BP.
又∵M、N分别为AD、BC边上的中点,且ABCD是正方形,
∴BP=PC.
∴BC=BP=PC.
∴△PBC是等边三角形.
∴PB=PC;
(2)证明:由(1)知△PBC是等边三角形.
∵PN⊥BC于N,BN=NC=$\frac{1}{2}$BC=$\frac{1}{2}$,∠BPN=$\frac{1}{2}$×∠BPC=30°,
∴PN=$\frac{\sqrt{3}}{2}$,MP=MN-PN=.
(3)证明:由折法知PQ=QC,∠PBQ=∠QBC=30°.
在Rt△BCQ中,QC=BC•tan30°=1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$,
∴PQ=$\frac{\sqrt{3}}{3}$.
∴以PQ为边的正方形的面积为$\frac{1}{3}$.
点评 本题考查了正方形的性质,翻折变换.解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
16. 若有理数a、b在数轴上的位置如图所示.则b+(-a)的值( )
若有理数a、b在数轴上的位置如图所示.则b+(-a)的值( )
 若有理数a、b在数轴上的位置如图所示.则b+(-a)的值( )
若有理数a、b在数轴上的位置如图所示.则b+(-a)的值( )| A. | 大于b | B. | 小于0 | C. | 小于a | D. | 小于b |
20.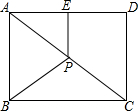 如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
 如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )| A. | 14 | B. | 16 | C. | 17 | D. | 18 |
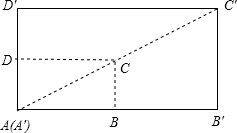 如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2.求AB和AD的长.
如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2.求AB和AD的长.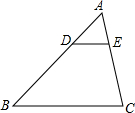 如图△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{4}$,求:
如图△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{4}$,求: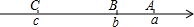 如图,已知A,B,C三点分别对应数轴上的实数a,b,c,化简:|a-b|+|c-b|+|c-a|.
如图,已知A,B,C三点分别对应数轴上的实数a,b,c,化简:|a-b|+|c-b|+|c-a|.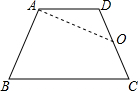 四边形ABCD为梯形,如图所示,其中AD∥BC,O为一腰中点.
四边形ABCD为梯形,如图所示,其中AD∥BC,O为一腰中点.