题目内容
直角坐标系中,直线l是第一、三象限的角平分线.已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,则Q点坐标 .
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:由轴对称性作出满足条件的Q点,求出直线D′E的解析式,与直线y=x联立,可求Q点的坐标,得出结论.
解答: 解:作D关于直线l的对称点D′,
解:作D关于直线l的对称点D′,
∵直线l是第一、三象限的角平分线.
∴直线l的解析式为y=x,则D(1,-3)关于直线l的对称点D'的坐标为(-3,1),连接D'E交直线l于点Q,此时点Q到D、E两点的距离之和最小;
设过D'(-3,1)、E(-1,-4)的设直线的解析式为y=kx+b,
则
,
∴
∴直线D′E的解析式为:y=-
x-
.
由
得
,
∴所求Q点的坐标为(-
,-
).
故答案为(-
,-
).
 解:作D关于直线l的对称点D′,
解:作D关于直线l的对称点D′,∵直线l是第一、三象限的角平分线.
∴直线l的解析式为y=x,则D(1,-3)关于直线l的对称点D'的坐标为(-3,1),连接D'E交直线l于点Q,此时点Q到D、E两点的距离之和最小;
设过D'(-3,1)、E(-1,-4)的设直线的解析式为y=kx+b,
则
|
∴
|
∴直线D′E的解析式为:y=-
| 5 |
| 2 |
| 13 |
| 2 |
由
|
|
∴所求Q点的坐标为(-
| 13 |
| 7 |
| 13 |
| 7 |
故答案为(-
| 13 |
| 7 |
| 13 |
| 7 |
点评:本题考查了一次函数的综合运用.关键是由轴对称的知识,结合图形,得出关于直线y=x轴对称的两点坐标关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a3<0,b2≥0,那么关于ab的值下列说法正确的是( )
| A、ab>0 | B、ab<0 |
| C、ab=0 | D、以上都可能 |
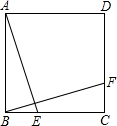 如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则α=( )
如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则α=( )| A、60° | B、90° |
| C、120° | D、45° |
已知A、B、C、D依次是直线AD上的4个不同点,则下列说法正确的是( )
| A、线段AD与线段BC是两条相同线段 |
| B、直线AD与直线BC是两条不同直线 |
| C、射线AB于射线AD是两条相同射线 |
| D、射线BC于射线BD是两条里不同射线 |
