题目内容
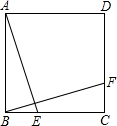 如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则α=( )
如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF,将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则α=( )| A、60° | B、90° |
| C、120° | D、45° |
考点:旋转的性质
专题:计算题
分析:连结AC和BD,它们相交于点O,如图,根据正方形的性质得到AB=AC,∠AOB=90°,由于△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α,则根据旋转的性质得α=∠AOB=90°.
解答:解: 连结AC和BD,它们相交于点O,如图,
连结AC和BD,它们相交于点O,如图,
∵四边形ABCD为正方形,
∴AB=AC,∠AOB=90°,
∵△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α,
∴△ABC中点A与△BCF中的点B是对应点,
∴α=∠AOB=90°.
故选B.
 连结AC和BD,它们相交于点O,如图,
连结AC和BD,它们相交于点O,如图,∵四边形ABCD为正方形,
∴AB=AC,∠AOB=90°,
∵△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α,
∴△ABC中点A与△BCF中的点B是对应点,
∴α=∠AOB=90°.
故选B.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
在1,-1,-2这三个数中,把其中任意两个数相加,和最小的是( )
| A、1 | B、0 | C、-1 | D、-3 |
甲、乙、丙三地海拔高度分别为20米,-14米,-9米,那么最高的地方比最低的地方高( )
| A、34米 | B、29米 |
| C、11米 | D、6米 |
下列调查,比较适合采用普查方式的是( )
| A、调查海尔某种型号数字电视机的使用寿命 |
| B、调查中央电视台《开讲了》栏目的收视率 |
| C、调查全国中学生的体重 |
| D、调查你们班同学的身高 |
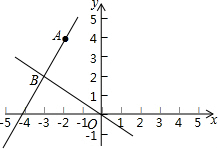 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-