题目内容
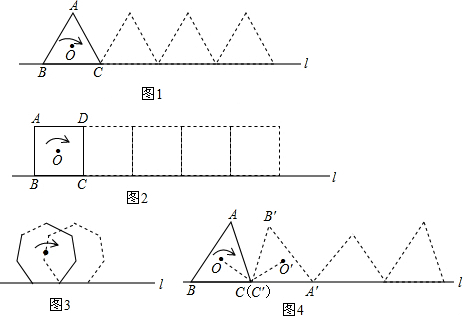
(1)如图1,设正三角形ABC的外接圆圆心为O,半径为R,将其沿直线l向右翻滚,当正三角形翻滚一周时,其圆心O经过的路程是多少?
(2)如图2,设正方形ABCD的外接圆圆心为O,半径为R,将其沿直线l向右翻滚一周,其圆心O经过的路程是多少?
(3)猜想:如图3,设正多边形的外接圆圆心为O,半径为R,将其沿直线l向右翻滚一周,其圆心O经过的路程是多少?请说明理由.
(4)进一步猜想:任何一个三角形都有一个外接圆(设外接圆的半径为R),若将该三角形翻滚一周,其外接圆圆心所经过的路程是否是一个定值?为什么?请以任意三角形为例说明(如图4).
(2)如图2,设正方形ABCD的外接圆圆心为O,半径为R,将其沿直线l向右翻滚一周,其圆心O经过的路程是多少?
(3)猜想:如图3,设正多边形的外接圆圆心为O,半径为R,将其沿直线l向右翻滚一周,其圆心O经过的路程是多少?请说明理由.
(4)进一步猜想:任何一个三角形都有一个外接圆(设外接圆的半径为R),若将该三角形翻滚一周,其外接圆圆心所经过的路程是否是一个定值?为什么?请以任意三角形为例说明(如图4).

考点:圆的综合题
专题:
分析:(1)当正三角形ABC向右翻滚一周时,其中心O经过的路线是三条等弧,根据弧长公式求出一条弧长,继而可得出答案.
(2)滚过的路程相当于4个90°的圆弧的长,继而代入弧长公式计算即可.
(3)当n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所对的圆心角为
,继而代入计算即可.
(4)是定值2πR,按照前面的计算思想进行证明即可.
(2)滚过的路程相当于4个90°的圆弧的长,继而代入弧长公式计算即可.
(3)当n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所对的圆心角为
| 360° |
| n |
(4)是定值2πR,按照前面的计算思想进行证明即可.
解答:解:(1)当正三角形ABC向右翻滚一周时,其中心O经过的路线是三条等弧,
所以其中心O经过的路程为:
×3=2πR.
(2)中心O经过的路程为
×4=2πR.
(3)当n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所对的圆心角为
,
所以中心O经过的路程为
×n=2πR.
(4)是定值2πR,理由如下:
在△ABC中,设∠A=α,∠B=β,∠C=γ,△ABC的外接圆⊙O的半径为R,
把△ABC沿直线l向右翻滚一周时,其外心O经过的路线是三条弧,
当AC边与直线l重合时,C与C'重合,A与A'重合,B与B'重合,
连接CO、C'O',则∠ACO=∠A'C'O',
所以∠OCO'=∠ACA'=180°-γ,
所以l=
,
同理,另两条弧长分别为:
,
,
所以外心O所经过的路程为2πR.
通过以上猜想可得结论为:把圆内接多边形翻滚一周时,多边形的外心所经过的路程是一个定值.
所以其中心O经过的路程为:
| 120πR |
| 180 |
(2)中心O经过的路程为
| 90πR |
| 180 |
(3)当n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所对的圆心角为
| 360° |
| n |
所以中心O经过的路程为
| ||
| 180 |
(4)是定值2πR,理由如下:
在△ABC中,设∠A=α,∠B=β,∠C=γ,△ABC的外接圆⊙O的半径为R,
把△ABC沿直线l向右翻滚一周时,其外心O经过的路线是三条弧,
当AC边与直线l重合时,C与C'重合,A与A'重合,B与B'重合,
连接CO、C'O',则∠ACO=∠A'C'O',
所以∠OCO'=∠ACA'=180°-γ,
所以l=
| (180-γ)πR |
| 180 |
同理,另两条弧长分别为:
| (180-α)πR |
| 180 |
| (180-β)πR |
| 180 |
所以外心O所经过的路程为2πR.
通过以上猜想可得结论为:把圆内接多边形翻滚一周时,多边形的外心所经过的路程是一个定值.
点评:此题考查了圆的综合题,弧长的计算,解答本题的关键是掌握一些特殊图形的性质,熟练记忆弧长公式,有一定的难度,注意培养猜测、推理能力.

练习册系列答案
相关题目
下列命题是真命题的是( )
| A、方程3x2-4=2x的二次项系数为3,一次项系数为-2,常数项为-4 |
| B、同一时刻在阳光照射下,物体越长,地面上的影子越长 |
| C、四个角都是直角的两个四边形一定相似 |
| D、某种彩票中奖的概率是1%,买100张该种彩票一定会中奖 |
 如图,在直角坐标系中,矩形ABCD的顶点,A的坐标为(1,0),对角线的交点P的坐标为(
如图,在直角坐标系中,矩形ABCD的顶点,A的坐标为(1,0),对角线的交点P的坐标为(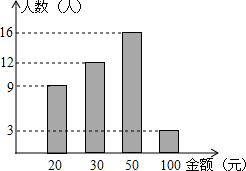 春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.
春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图. 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线